ベクトル場の発散

∗ベクトル場の発散
∗発散の式の導出
∗発散の物理的な意味
∗その他のベクトル場
 ・ベクトル\(f=ρv\) (質量)
 ・ベクトル\(E\) (電場)

∗ 例題：ベクトルの発散を求める

∗ ラプラシアン \(∆\)

∗【閑話】
 電場の発散の式❹の導出
 電場と電位について

 ベクトルの場の発散 

(※):「\( div \bv{f} = ∇\cdot \bv{f}\) :❶'」 の導出　
演算子\(∇\)は \(∇=(\pder{}{x},\pder{}{y},\pder{}{z})\)でした。

\(\underline{ div \bv{f} \ }\)\(=\pder{}{x}f_x+\pder{}{y}f_y+\pder{}{z}f_z\)
これは以下のように内積の形で表せる。
\(=(\pder{}{x},\pder{}{y},\pder{}{z}) \cdot (f_x,f_y,f_z)\)
\(\underline{=∇ \cdot f} \)

 物理での発散例は電場(E)の発散、磁場の発散(B)、流体の発散などあります。
ここでは流体を例にして説明していきます。
以下の\(f\)は速度ベクトルで考え、また流体(非圧縮性)が流れている水路をイメージする。
fig1 は配管の中の微小直方体である、微小面に対して速度は一様であるとする。
ベクトル\(\bv{f}\)の成分は：

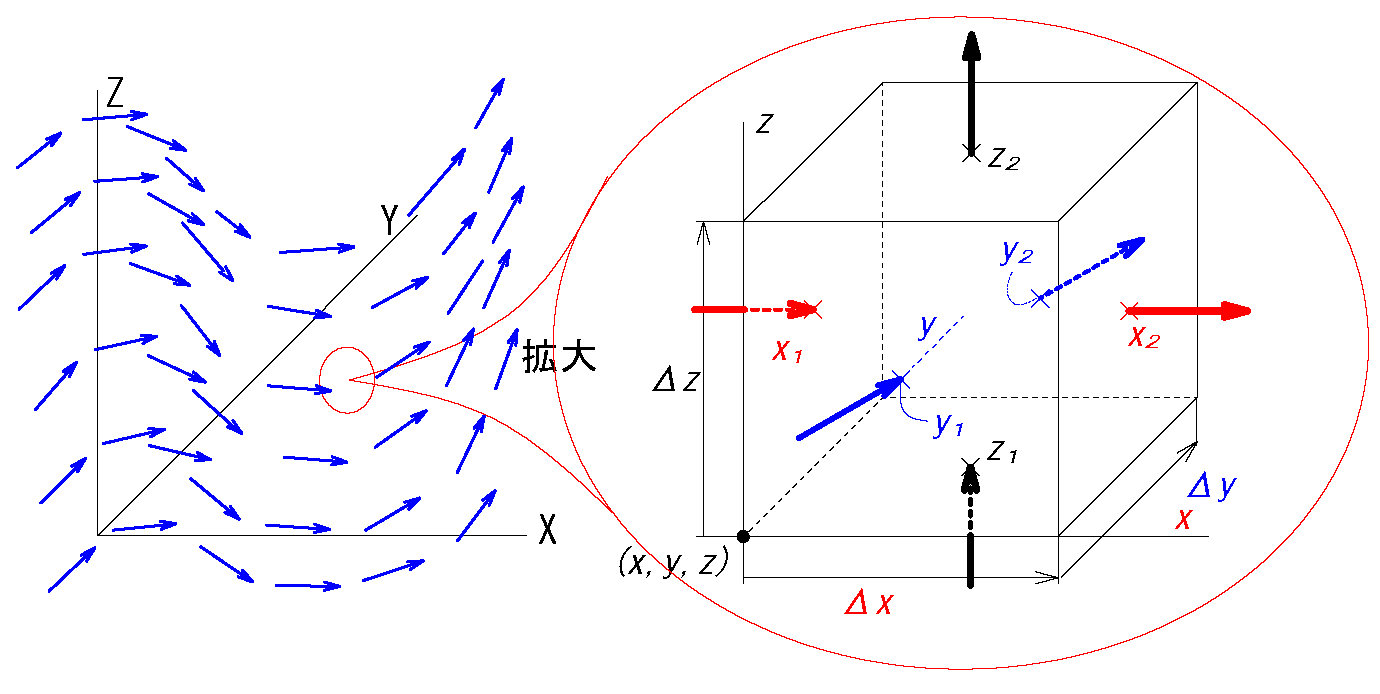
\(\bv{f}(x,y,z) \) \(=(\ f_x \s{(x,y,z)},f_y \s{(x,y,z)},f_z \s{(x,y,z)} \ ) \)

この微小部に流れ込む流量(体積)と流れ出る流量を計算する。
\(X_1\)から流入して\(X_2\)へ流出する流量 \(Q_x\) ：

\(X_1\)での流速を\(f_x(x,y,z)\)　\(,\) \(X_2\)での流速を\(f_x(x+Δx,y,z)\)
考えている面では流速一定である。（微小部の面だから）
\(Q_x= \s{ (f_x (x+Δx,y,z)-f_x (x,y,z) )ΔyΔz } \)

\(Y_1\)から流入して\(Y_2\)へ流出する流量 \(Q_y\) ：

\(Y_1\)での流速を\(f_y(x,y,z)\)　\(,\) \(Y_2\)での流速を\(f_y(x,y+Δy,z)\)
\(Q_y=\s{ (f_y (x,y+Δy,z)-f_y (x,y,z) )ΔxΔz }\)

\(Z_1\)から流入して\(Z_2\)へ流出する流量 \(Q_z\) ：

\(Z_1\)での流速を\(f_z(x,y,z)\)　\(,\) \(Z_2\)での流速を\(f_z(x,y,z+Δz)\)
\(Q_z=\s{ ( f_z (x,y,z+Δz) -f_z(x,y,z) )ΔxΔy }\)

  導出1   極限と偏微分から
\(Q=Q_x+Q_y+Q_z\)
各成分を「\(ΔxΔyΔz\)」で割る

\(\frac{ ( f_x(x+Δx,y,z)-f_x(x,y,z)　)ΔyΔz } {ΔxΔyΔz}\)\(=q_x\)

\(\frac{(f_y(x,y+Δy,z)-f_y(x,y,z))ΔxΔz } {ΔxΔyΔz}\)\(=q_y\)

\(\frac{(f_z(x,y,z+Δz)-f_z(x,y,z) )ΔxΔy}{ΔxΔyΔz}\)\(=q_z\)

以下、\(q_x\)について解く:

\(q_x=\frac{f_x(x+Δx,y,z)-f_x(x,y,z)}{Δx} \)

次に「Δx→0」とする極限をとる。

\(\displaystyle \lim_{Δx \to 0 } \frac{f_x(x+Δx,y,z)-f_x(x,y,z)}{Δx}\) \(=\pder{f_x}{x}\)

上式での\(y,z\) は定数。
同様に\(q_y\) と \(q_y\) についての極限を求め加算すると：
\(q=q_x+q_y+q_z\) の各項を各成分について偏微分したものである。

\(\underline {\pder{f_x}{x}+\pder{f_y}{y}+\pder{f_z}{z}}\) \(\ :❷\)

これは単位体積当たりの流量の変化量である。
さらに以下の如く展開できて、発散の定義が導出できる。

\(\pder{f_x}{x}+\pder{f_y}{y}+\pder{f_z}{z}\) \(=\pder{}{x}f_x+\pder{}{y}f_y+\pder{}{z}f_z\)
\((\pder{}{x},\pder{}{y},\pder{}{z})\)\( \cdot \ (f_x, f_y, f_z)\) \(=∇ \cdot \bv{f}\)\(=div \ \bv{f}\)

 導出2  テイラー展開を利用
次に\( f_x(x+Δx,y,z)\) のテイラー展開の一次近似を求める。

1変数のテイラー展開の一次近似式
\(f(x) \simeq f(a)+\frac{f'(a)}{1!}(x-a)\)
上式を変形する。( \(x \rightarrow x+Δx\)　\(\ ,\)　\( \ a \rightarrow x\) )
\(f(x+Δx) \simeq f(x)+f'(x)Δx\)
従い \( f_x(x+Δx,y,z)\) のテイラー展開の一次近似式は：
\( f_x(x+Δx,y,z) \simeq f_x(x,y,z)+\pder{f_x}{x}Δx \)

これより流出する流量は：

\(Q_x=[f_x(x+Δx,y,z)-f_x(x,y,z)]ΔyΔz\) \( = [\cancel{f_x(x,y,z)}+\pder{f_x}{x}Δx\)\(-\cancel{f_x(x,y,z)}]ΔyΔz\)
\(Q_x=\pder{f_x}{x}ΔxΔyΔz\)

同様にして\(Q_y\),\(Q_z\)を求めて、\(Q=Q_x+Q_y+Q_z\)とすると：

\(Q=\pder{f_x}{x}ΔxΔyΔz+\pder{f_y}{y}ΔxΔyΔz\)\(+\pder{f_z}{z}ΔxΔyΔz\)
\(Q=(\pder{f_x}{x}+\pder{f_y}{y}\)\(+\pder{f_z}{z})ΔxΔyΔz\)

上式を体積\(ΔxΔyΔz\) で割ると、

\(\underline{ \pder{f_x}{x}+\pder{f_y}{y}+\pder{f_z}{z} }\)

上記の式❷と同じ式が導かれた。…<導出終わり>

 はじめに,上述の続きとして、流体の流速ベクトルをもとにした流量の変化の例を説明します。
その次に流体の質量の変化の例、さらに電場における電荷と電流密度の例を説明します。
マクロ的には流体の例でも電磁気の例も同じようだが、詳細は異なることがあるので留意して下さい。
（詳しくはその分野に進んで学ぼう！）
ここでの目的は数学の「ベクトルの分散」を理解することです。

 fig1 は,曲がりくねった水路、配管などの微小部分です。
また非圧縮性流体の前提だから膨張も圧縮もないので以下のことが言えます。
\( div \ \bv{f}=\pder{f_x}{x}+\pder{f_y}{y}+\pder{f_z}{z} \:❷　　\)
この式の x軸方向について説明する(上記の第1項)：

微小部に流入する量\(q_i\)と微小部から流出する量\(q_o\)とすると：
式❷第1項は \(\frac{q_o-q_i}{Δx}\)という(微分のときの)変化率の形の式に対し、 \(Δx \rightarrow 0\)での偏微分、それが式❷である。
\(\displaystyle \lim_{Δx \to 0 } \frac{q_o-q_i}{Δx}\)\(=\pder{f_x}{x}\)

従い、発散は流出量が多い「\(q_o \gt q_i\)のとき、正」である。
発散は次のパターンがある。
・\(div \ \bv{f} \gt 0\)：湧き出し

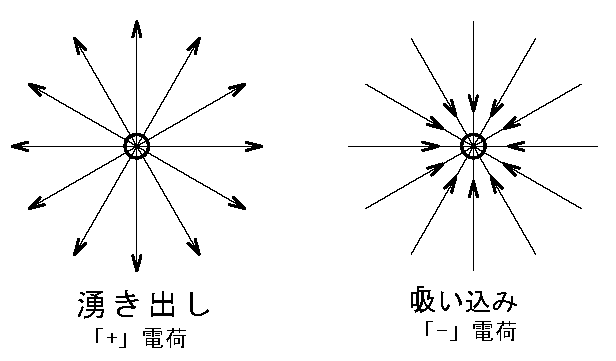
水路の途中に湧き水がある。
(入る量\(\lt\)出る量)

・\(div \ \bv{f} \lt 0\)：吸い込み

水路の途中に排水(吸い込み)されている。
(入る量\(\gt\)出る量)

・\(div \ \bv{f}=0\):湧き出し無し（出入り一定）。

変化が無い(微分が0)ことは、物理の保存則が働いている。（エネルギーの保存則のように）
(入る量\(＝\)出る量)

上の説明では非圧縮性の流体であったが、現実的に圧縮、膨張性の流体とし、そのため密度 \( ρ(x) \small{ (kg{/}m^3) } \)を導入する。
簡単のため次のようにする。
・関数\(ρ,\bv{v}\)は\((x,y,z,t) \)の関数だが、ここでは\(x,t\)の関数とする。
・考えている曲面\(ΔS\) と\(f(x)=ρ\bv{v}\) は互いに垂直とする。
・従って流体は全て\(x\)軸方向に流入出する。
\(f(x)\)は単位時間当たりに曲面ΔSを通過(流出入)する流体の質量\(\bv{f(x)}=ρ\bv{v}\)である。
比重\(ρ\) は単位体積当たりの質量であり、\(∂ρ{/}∂t\) は単位体積当たりの質量の時間変化であることに留意する。
次がいえる：
単位体積当たりの質量の時間変化＝単位時間当たり、単位体積に流出入する質量の発散
これから次の式が成り立つ。

\(\pder{}{t}ρ =-div\ ρ\ \bv{v}\)　\(\ :❸\)
\(\pder{}{t}ρ + div\ ρ\ \bv{v}=0\) \(\ :❸'\)

これは物理の質量保存の式です。
対象としている物質量が不滅のときに成り立つ式です。
・流体密度(の変化)が減ることは、流体の流れ出（湧き出し）がある。
・流体密度(の変化)が増えることは、流体の流れ込み（吸い込み）がある。
・流体密度の変化がないことは一定の流れである。（湧き出し無し）

関係する記号の説明

・\(E\):電場\(\small{(N/C)}\)  ・\(q\)：力を受ける電荷 \(\small{ (N) }\)
・\(Q\)：電場を作る点電荷　 　・\(ε_0\):真空の誘電率　\(\small{(c^2/Nm^2\ )}\)　
・\(k=\frac{1}{4\pi ε_0}\)  　・\(r\):距離　\(\small{(m)}\)
・\(ρ\):電荷密度=単位体積当たりの電荷　\(\small{(c/m^3\ )}\)
・\(\bv{j}\):電流密度ベクトル=単位面積、時間当たりに通過する電荷量　\(\small{(A/m^2\ )}\)
・\(D\):電荷密度\(C/m^2\), 真空中において\(D=ε_0E\)

下式はガウスの法則から導いたマックウェルの方程式（4式）のなかの１つである。

\(div E= \frac{ρ}{ε_0}\)　　\(\ :❹\)　
 または
\(div D= ρ\)　　\(\ :❹’\)　

導出はここでのテーマではありませんが参考として【閑話】の載せておきます。
この式は「電場の発散\(div E\)は電荷密度（電荷量）によって決まる」を示す。

次式は電荷保存の式と呼ばれている式です。
\( \pder{}{t}\ ρ(x) + div\ \bv{j}(x)=0\)　 \(\ :❺\)
前述した流体（質量）のベクトル場の式❸'とよく似ている。
\(\pder{}{t}ρ + div ρ\ \bv{v}=0\) \(\ :❸'\)

前述した質量保存則の「質量密度➝電流密度」を「流体→電荷」に換えて書くと以下となる。
これは 式❺ の物理的な意味となります。
(下記の電荷の流れとは電流のことです)
・電流密度(の変化)が減ることは、電荷の流れ出（湧き出し）がある。
・電流密度(の変化)が増えることは、電荷の流れ込み（吸い込み）がある。
・電流密度の変化がないことは定電流である。（湧き出し無し）
これは不生不滅となる電荷保存則です。

\( div f=\pder{}{x}(-yz) +\pder{}{y}(-x) +\pder{}{z}(-xy)\)\(=0\)

\( div f=\pder{}{x}(xy^2) +\pder{}{y}(xy^2) +\pder{}{z}(-x^2z^2)\) \(=y^2+2xy-2x^2z\)

スカラー関数\(f\)の勾配は

\(grad\ f=∇ｆ\) \(=(\pder{f}{x},\pder{f}{y},\pder{f}{z})\)

この結果はベクトル値関数だから発散をとることができます。

関数\(f\)の勾配ベクトルの発散

\(div\ (grad\ f\ ) \)\(=∇\cdot (grad\ f)\)\(=∇\cdot\ (∇f) \)\(=∇\cdot ∇\ f \)
\(=(\pder{}{x},\pder{}{y},\pder{}{z})\)\(\cdot\) \( (\pder{f}{x},\pder{f}{y},\pder{f}{z})\)
上式を内積演算すると：
\(= \pder{}{x}(\pder{f}{x})+\pder{}{x}(\pder{f}{y})+ \pder{}{z}(\pder{f}{z}) \)
\(= \pdera{f}{x}+\pdera{f}{y}+ \pdera{f}{z}\)
\(= \color{red}{ (\pdera{}{x}+\pdera{}{y}+ \pdera{}{z})\ } f\)
これを次のように書く
\(=\color{red}{ ∆} \ f\)

すなわち:
\(\color{red}{∆}=∇\cdot ∇=∇^2\)\(= (\pdera{}{x}+\pdera{}{y}+ \pdera{}{z}) \)

\(∆\)はラプラシアンまたはラプラス演算子という。

記号の「\(∇\)」と「\(∆\)」を間違えないように！
・\(∇\)：1階微分演算子
・\(∆\)：2階微分演算子
微分方程式のラプラス変換、電磁気学、力学などを学んいて、この「ラプラシアン\(∆\)」 が出てきたら、ここを思い出して下さい。

関係する記号の説明

・\(E\):電場\(\small{(N/C)=(V/m)}\) ⓐ(以下で確認する)
・\(q\)：力を受ける電荷   ・\(Q\)：電場を作る点電荷
・\(ε_0\):真空の誘電率　\(\small{(c^2/Nm^2\ )}\)　
・\(k=\frac{1}{4\pi ε_0}\)  　・\(r\):距離　\(\small{(m)}\)
・\(ρ\):単位体積当たりの電荷　\(\small{(c/m^3\ )}\)

電場E は次のように電荷Q に比例する。

\(E\)\(=k\frac{Q}{r^2}\) \(=\frac{1}{4\pi ε_0}\frac{Q}{r^2}\) \(=\frac{1}{4 \pi r^2}\frac{Q}{ε_0}\) \(\ :(a)\)
\(4 \pi r^2 \cdot E=\frac{Q}{ε_0}\)
\(4 \pi r^2 =S\)：球体の表面積、 \( \frac{Q}{ε_0}\)=定数
式(a)に面積S を掛ける
\(\underline{ S \cdot E=\frac{Q}{ε_0} }\)\(\ :(b)\)

以上は球面\(S\)の閉曲面からの湧き出しである。　これを一般の閉曲面\(S\)として、
微小面積\(dS\)の法線単位ベクトルを\(\bv{n}\)とすると：
\(\underline{ \displaystyle \int_S E \cdot n dS= \frac{Q}{ε_0}=\displaystyle \int_V ρ \frac{1}{ε_0} dV}\) \(\ :(c)\)

\(( Q= \frac{1}{ε_0} dV) \)

ここで、以下のガウスの法則を受け入れて：
\( \displaystyle \int_V div f dV= \displaystyle \int_S f\cdot n dS \)

より、式 (c) は：
\(\displaystyle \int_s E\cdot n ds\) \(=\displaystyle \int_V div E\ dV= \frac{Q}{ε_0}\)\(=\displaystyle \int_V ρ \frac{1}{ε_0} dV\)
\(\therefore \underline{ div E= \frac{ρ}{ε_0} }\)　\( :(d)\)
以上、電場\(E\)の発散とガウスの法則から導きました。
電場の発散\(div E\)は電荷密度（電荷量）によって決まることを意味しますね。

電場Eとは電荷\(q\) が電気的な力を受ける空間のことで、ある点で試験電荷（+1Cの正電荷）が受ける静電気力(ベクトル)で表す。
電位V とは+1c の電荷\(q\)が持つ静電気力の位置エネルギー(スカラー)のことである。
力学の「重力に逆らって質量m を高さh(m) に持上げる仕事を重力の位置エネルギー mghである 」と電位はよく似ている。

+1C の電荷が「電場E(N/m=V/m)の静電気力が働いている状態にある」をイメージすると：

電位とは「0V の基準位置からの距離 r(m)にある+1C の電荷の位置エネルギーが V=1・E・r＝Er(V）」のことです。
（+1C の電荷は電場E に逆らってr (m) 動かす仕事に相当する位置エネルギー（電位）はV=Er(V）である。）