湘南理工学舎・物理数学・全微分（1変数）・接線

（1変数の微分係数の応用）

本講では2変数(空間)での「曲面と接平面」を学ぶ準備として、１変数（平面）での「曲線と接線」について復習をします。
曲線のある点での接線の傾きは微分係数です。
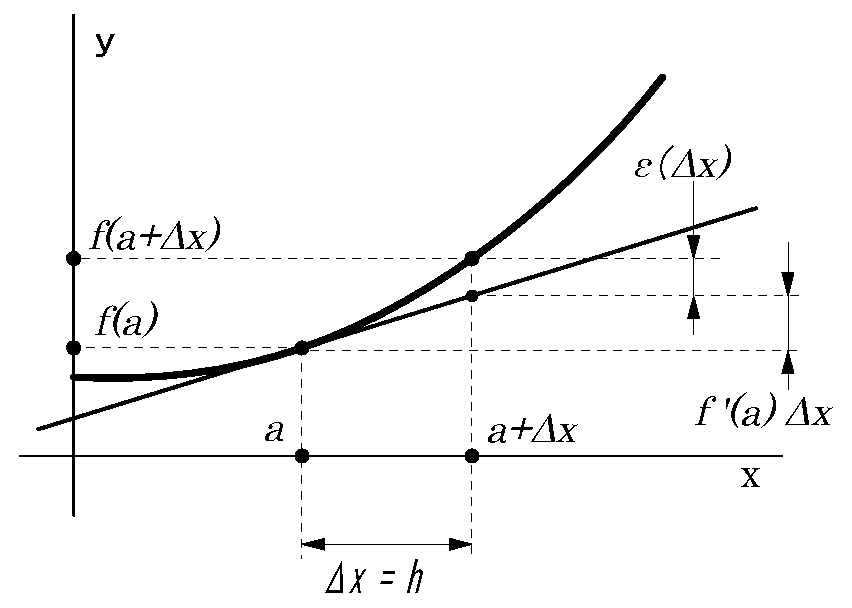
　図は1変数関数の曲線とその点における傾き（接線）を表わしています。
この傾きが微分係数です。微分係数の定義式は:

\( f’(a) = \lim_{\varDelta x \to 0}\frac{ f(a+\varDelta x) - f(a) }{\varDelta x} \) \(=\lim_{\varDelta x \to 0}\frac{ \varDelta y }{\varDelta x} \)

さらに図のε（∇\(x\)) は次のように考える。

\( f(a+\varDelta x)-f(a) = f'(a) \varDelta x + ε(\varDelta x) \)

上式の両辺をhで割って、\(　\varDelta x　\)を限りなく0に近づけると、微分係数の定義から

\( \lim_{\varDelta x \to 0} \frac{ε(\varDelta x)}{\varDelta x }　= 0 \)

であるから

\( \lim_{\varDelta x \to 0}\frac{ f(a+\varDelta x)-f(a)}{\varDelta x} \)

\( = f'(a) + \lim_{\varDelta x \to 0} \frac{ε(\varDelta x)} {\varDelta x }\) \(= f'(a)\)

　となります。
上の最後の式は \( \ \frac{0}{0} \ \) の不定形であるが、上記より0に収束、すなわち極限値の答えが 0 である。　
0 になることは ε(\( \varDelta x\))は\(\varDelta x\)より高位の無限小であることを示している。
（ε(\( \varDelta x\))が\(\varDelta x\)より早く0に収束する。）
\( a+\varDelta x \)を\(a\) に限りなく近づければ ε(\( \varDelta x\))は0となり、接線の傾きに収束します。

また接線の方程式は\(　f'(a)=m \) とすると

\( y-f(a)= f'(a)(x-a)= m(x-a) \)

（ここであえて2変数の微分表記の\( \frac{\partial f}{\partial x} \)を使っています）
1変数関数\(ｆ\)の変化量\(\varDelta f\)は直線の傾きを\( \frac{\partial f}{\partial x} \)の形で表す。さらに区間\( \varDelta x \)を限りなく小さくし、\( \varDelta x →dx　、\varDelta f →df \)にして変形すると見慣れた全微分式となる。

\( \varDelta f=\frac{\partial f}{\partial x}\varDelta x +\frac{\partial f}{\partial y} \varDelta y(=0)\) \(＝\frac{\partial f}{\partial x} \varDelta x \quad \dotsm\)

\( \therefore df =　\frac{df}{dx} dx \)

ある点x=aでの傾き(微分係数）とすると

\( \left. df \right |_{ x = a }=\) \(\left. \frac{ dy }{ dx } \right|_{ x = a } dx\) \(= f'(a)\ dx = m\ dx \)

ｍは点Aにおける傾きで定数であるから上式（1変数の全微分式）は直線となる。

coffe

[コーヒーブレイク/閑話］…接線の概念が曲線の曲率に！

ここで曲線の接線と曲線の曲率を見ていきましょう。

曲線上の近接している2点での接線が交差する角度は曲線の曲がり具合を示しています。…これが出発点です。
2次元では曲線と接線の関係ですが、3次元ではどうなるか…曲面と接平面が対応すると推測されるが……これについては後の講義で取り上げます
下図は平面の曲線と接線と微小な弧について描いています。

曲率は曲線の曲がり具合を表している、図の点Dは曲率が小さく（曲がりが小さい）、点Cは曲率が大きい。（曲がりが大きい）
そして曲率κは今、学んだ「接線」を用いて次式で計算できます。

\( κ　= \lim_{B \to A} \ \ \frac{α}{h_{AB}} \)

曲線のABの弧の長さ　\( {h_{AB}} \)は、Aの接線とBの接線のなす角 α とします。
BをAに近づけるように回転させると、Bの接線はAの接線と平行になろうとする。
このようにBをAに近付けて、2つの接線のなす角 α と弧の長さ\( {h_{AB}} \) の比の値の極限を曲線の点Aでの曲率という。
ここでの弧は円弧でないが、十分小さな領域なら円弧に近似できるので、κ　の逆数を曲率半径と呼んでいる。

曲線と接線・全微分

図1. 曲線と接線

[コーヒーブレイク/閑話］…接線の概念が曲線の曲率に！

ここで曲線の接線と曲線の曲率を見ていきましょう。

【曲線の接線と曲率】