保存則とは?
状態(通常は時間)が変化しても, ある物理量の値が変化しないことを保存の法則(以下保存則)と呼ぶ。
古典力学での保存則の代表は
1. 運動量保存則
2. エネルギー保存則
3. 角運動量保存則
である。何か新しい法則があるようにも思えるが, あえて誤解を恐れずに言えば, 唯一の法則は「
作用・反作用の法則」のみである。
上記3保存則は全て作用・反作用の法則から導かれる。新しい事実は無い。ではなぜわざわざ保存則と命名するのか?
① その量を導入することにより, 著しく計算が短縮される。(筆者の主観です)
② 個々の系の性質ではなく, 運動の法則, 力の性質がもたらすものであり, 普遍的に成り立つ。
からである。実際は法則という名誉称号をもらっている理由は②であるが, 順に説明してゆこう。
力積
運動量が保存される状況を簡単に説明しよう。運動量 \(m \upsilon~\)の変化は, 質量は一定として
\[\begin{align}
m \triangle \upsilon &=m \frac{\triangle \upsilon}{\triangle t} \triangle t \\ &=ma \triangle t \\
&=F \triangle t \tag{1} \\
\end{align}\]
すなわち, 運動量の変化はその間に加えられた力\(\ F\)と時間\(\triangle t\)の積である。
\(F \triangle t \)を
力積という。
\((1)\)の形式で表した運動を
運動量原理とも呼ぶ。原理の意味が分かり難いが, 運動方程式\(~F=ma\)を力学の原理と呼ぶと, 運動量原理と呼ぶのがふさわしい位の意味である。
実はニュートンがプリンピキアで述べているのは\(~F=ma\)ではなく, \((1)\)式の\(~\triangle p=F \triangle t~\)の方である。
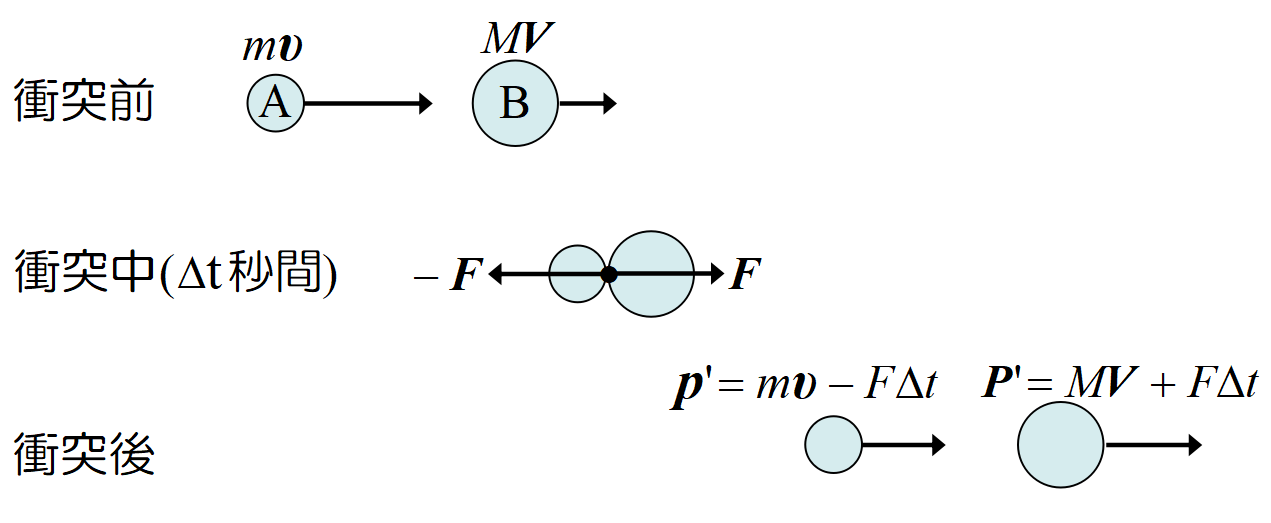
ここで図の様に質量, \(m, M\)の小球\(A\),\(B~\)が, 速度\(\bm{\upsilon}, V\)で運動しているとする。運動量はそれぞれ, \(m \bm{\upsilon}\), \(M\bm{V} \)である。
この2物体が\(\triangle t\)秒の間衝突したとする。
\(~A~\)が\(~B~\)に及ぼす力を\(~\Vec F~\)とすると, 作用・反作の法則により, \(B~\)が\(~A~\)に及ぼす力は\(-\Vec F~\)である。衝突時間\(\triangle t\)は共通であるから, \(~A~\)の運動量変化は\(~-\Vec F \triangle t\), \(~B~\)の運動量変化は\(~+\Vec F \triangle t\)である。
衝突後の全運動量は\(~\Vec p' + \Vec P' = m\bm{\upsilon} - \Vec F \triangle t + M \Vec V + \Vec F \triangle t = m\bm{\upsilon} + M \Vec V\)で, 衝突前と変わらない。
すなわち運動量保存則は作用・反作用の法則のことであり, 新しい事実は無い。
上記の例で分かるように, 注目している物体の外部からの力「
外力」の作用が無い限り, すなわち「
内力」のみの場合, 注目している物体系の全運動量は変わらない。これを運動量保存則と呼ぶ。
ここで改めてニュートン力学を見てみよう。
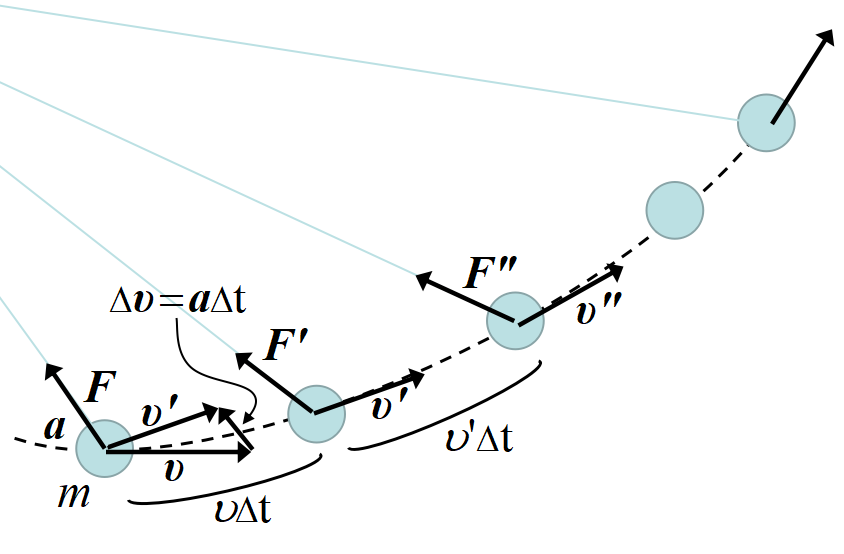
運動方程式は瞬間の表現
運動方程式
\[\Vec F=m\frac{\triangle\bm{\upsilon}}{\triangle t}\]
は, ある瞬間の状態の記述である。非常に短い時間\(\triangle t\)秒であれば, 力や加速度を一定と見ることができて, \(\triangle t~\)秒後の位置や速度を予想することができる。これを繰り返せば数か月先の惑星の位置を計算できるのであり, 事実人類はそうして観測事実を積み上げてきた。ニュートン力学は, 瞬瞬刻刻の事象を積み重ね, 将来を予測するのが基本的なスタイルである。
本題(運動量保存則)からは離れるが, 運動方程式を理論的に導き出す手立てはなく, 観測事実の積み重ねが,
運動方程式の正しさを担保していることを再確認しておこう。さて, 上記の方法で計算は出来るが, 膨大な手間と時間を要する。そこで積分という操作を導入する。
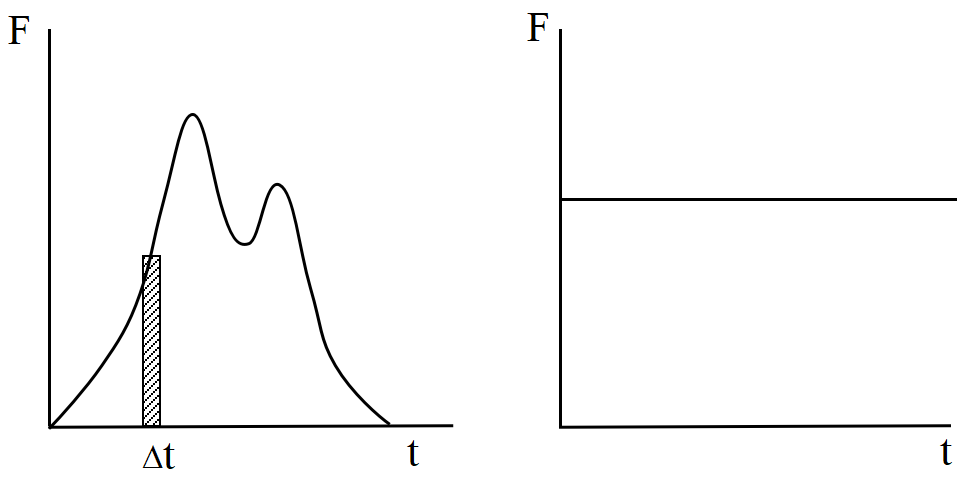
高校物理では\( F\)は一定としているが, 実際は時間の関数である場合が多い。そこで高校物理との違いを
「変化する力」なので積分が必要と積分を強調する記事が多い。極めて短時間では一定とみてよく, 同じように力積が計算できる。これを積み重ねればよいので, 積分は容易に理解できる。
運動方程式 (\(F=ma~\)と \(\triangle p = F \triangle t\)を適宜使い分ける)
\[\frac{d}{dt} m\Vec \upsilon = \Vec F \]
両辺を\(t_{1}\)から\(t_{2}\)まで積分すると
\[m\Vec \upsilon_{2}-m\Vec \upsilon_{1} = \int_{t_{1}}^{t_{2}} \Vec F(t) \,dt = \Vec I \tag{2}\]
\(\Vec I\)は力積\((Inpulse)\)である。説明の無い場合が多いが, 内力による力積と, 外力による力積を用いて \(\Vec I= \Vec I_{内}+ \Vec I_{外}\)とするのが正しい。
ここでベクトルの積分が出てくるが, 成分ごとの積分をまとめて書いただけである。例えば\(~x~\)成分は
\[m \upsilon_{2x}- m \upsilon_{1x} = \int_{t_{1}}^{t_{2}} F_{x}(t) \,dt\]
である。
\(\Vec I= \Vec I_{内}+ \Vec I_{外}\)の説明なしで, \(\Vec I= 0~\)のとき, \(m \Vec \upsilon_{2}= m \Vec \upsilon_{1}\)を運動量保存則としている説明を見かけるが, 正確ではない。運動量保存則とは, 最低でも2物体, 多くは多数の物体の衝突前後で, 運動量の総和が保たれることを言うので注意しよう。1つの物体で\(m \Vec \upsilon_{2}= m \Vec \upsilon_{1}\)は慣性の法則である。
いくつかの例を見てみよう。
1.1つの物体
力が働かない:\(\displaystyle \frac{d\Vec p}{dt}=0 → \Vec p = m \bm \upsilon = \)一定 (これは正しくは慣性の法則である)
質量変化する:\(\displaystyle \frac{d(m\bm\upsilon)}{dt}= \upsilon \frac{dm}{dt} +
m \frac{d \bm\upsilon}{dt}=0 → m\frac{d \bm\upsilon}{dt} =- \upsilon \frac{dm}{dt} \) (ロケットの推進力)
2. 2つの物体の重心の運動
質量\(~m\), \(M\), それぞれの座標が\(~x_{m}, x_{M}\)の2つの物体の重心の運動を考える。重心の座標\(~x_{G} \)は
\[x_{G}= \frac{mx_{m}+ Mx_{M}}{m+M}\]
である。重心の速度は,
\[
\begin{align}
\upsilon_{G} &=\frac{dx_{G}}{dt} \\
&=\frac{1}{m+M}\left(m \frac{dx_{m}}{dt}+ M \frac{dx_{M}}{dt}\right) \\
&=\frac{m \upsilon_{m}+M \upsilon_{M}}{m+M} \\
\end{align}
\]
で, \(m \upsilon_{m}+M \upsilon_{M}\)は系の全運動量であるから一定。
すなわち重心は等速度運動をする。最初に静止していれば, 重心は静止したままである。気象衛星ひまわりを打ち上げたロケットの重心は, ずっと種子島宇宙センターに留まっている。
内力と外力
さて, 内力, 外力と簡単に言ってきたが, 区別は意外と難しい。特に受験生にとっては重大である。実例で説
明しよう。
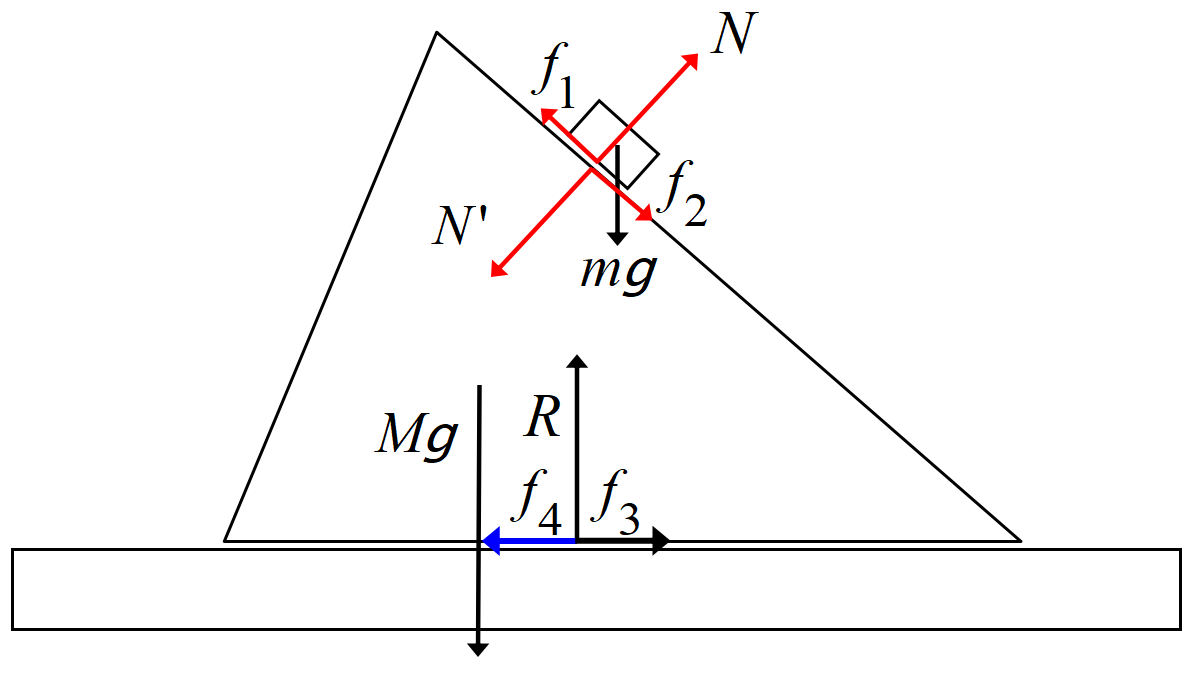
例1:質量\(~M~\)の斜面\(A~\)を,質量\(~m~\)の物体\(B~\)が滑り落ちる場合を考える。斜面と床, 斜面と小物体には摩擦があるとする。
小物体が斜面から受ける垂直抗力, 摩擦力を夫々\(~N~,f_{1}~\), その反作用を\(~N'~,f_{2}~\)、斜面
が床から受ける垂直抗力, 摩擦力を夫々\(~R,f_{3}\)とする。注目している物体を内側の物体, それ以外を外側の物体とする。このとき内側の物体同士に働く力が内力, 外側の物体から受ける力が外力である。
さて\(f_{3}\)に対する反作用\(f_{4}\)(青色矢印)にふれないのは何故か?
内力, 外力と言うときは, 他の物体から受ける力であって, 他の物体に作用する力ではないからである。
今\(A+B\)に注目すれば, 床からの力\(R, f_{3}\), 地球からの力\(mg, Mg\)は外力である。図の赤色矢印が内力, 黒色矢印が外力である。この図の場合, 垂直方向の外力は釣り合っていて\(~0~\)であるが, 摩擦力\(~f_{3}~\)が働いているから, \(A+B~\)の系の運動量は保存されない。
例2:
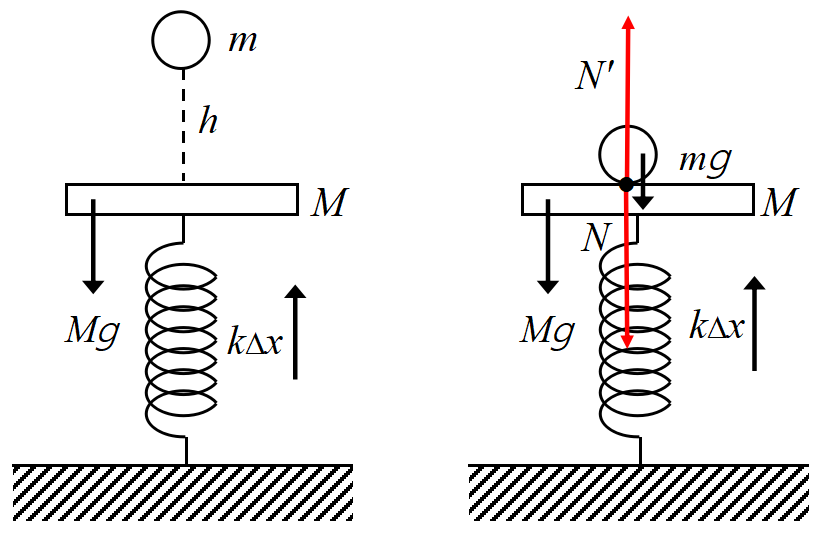
撃力近似 高さ\(~h~\)にある小物体が台に衝突した後の, 台の単振動の振幅と周期を求める問題である。
運動量保存則, エネルギー保存則, 弾性エネルギー, 単振動等, 力学の重要法則や基本的概念のほとんどすべ
てを含んでおり, 受験生の能力を知るのに格好の問題である。
衝突した瞬間の力を書き出してみよう。
台が受ける力は①小物体\(m\)から受ける撃力\(N\) ②重力\(Mg\) ③バネからの弾性力\(k \triangle x\), 小物体が受ける力は①撃力\(N\)の反作用\(N'\) ②重力\(mg\)である。小物体と台を一つの系とした場合, バネ, 地球は外部の物体であるから, 赤色矢印が内力, 黒色矢印が外力である。よく見ると重力\(mg\)が釣り合いから外れ残っている。すなわち外力が働いているので衝突において運動量は保存されない。がそれでは問題は解けない。
正解は「
衝突時間は極めて短く, 重力の影響は無視できる」ので運動量保存則は成り立
つである。この注釈を入れるかどうかを巡っての議論がある。(藤島 条件不足で解けない入試問題)
なまじ注釈を入れると, \(mgh\)はどうなるんだ?との誤解を受ける可能性もある。撃力近似の解答例として藤島は次の4つの例を挙げている。
(1) 設問の意味が分からず迷わずギブアップ。論外。
(2) 衝突と聞いて迷わず(馬鹿の一つ覚えともいう)運動量保存則を適用。正解の可能性も高い。
(3) 外力の働いていることを認識するが, 解決策が見つからずギブアップ。
(4) 外力が働いているので?と思うが, 入試問題に解答不能はありえないと考え運動量保存則を適用。
果たして筆者はどうであったろうか?と思わず考えてしまった。(2)かな?