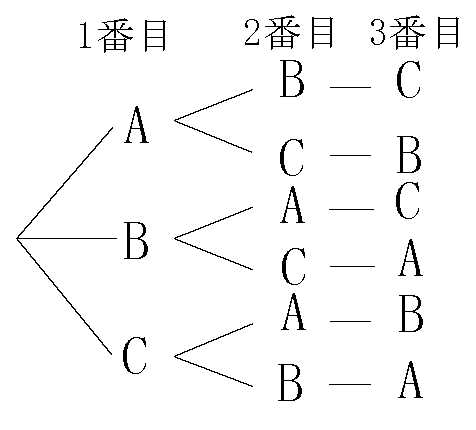
・1番目は「A, B,C 」の 3 通り。
・2番目は1番目の各々について2 通り。
・3番目は2番目の各々について1 通り。
この全並べ方は
\(3 \times 2 \times 1 = 6\) 通りです。
これを拡張して、次にカードが
4枚(A,B,C,D )の場合の:
全並べ方は
\(\color{red}{4} \times 3 \times 2 \times 1 = 24\) 通りとなります。
これは階乗の計算ですね。
一般に n 個のものを1列に並べる仕方は次の階乗で表せる。
❷:\( \underline{ n!=n・(n-1) \cdots 3・2・1} \)
\( n=0\) の時、\( 0!=1 \)と定義します。
結論をはじめからいうと、この並べ方を順列といいます。
重複を許さないが順序は考慮する並べ方です。
5人の名前はA,B,C,D とします。
\(\fbox{A}\ \fbox{B}\ \fbox{C}\ \fbox{D}\ \fbox{E} \)
1人目にはA~B の 5 人が入る。(2人目は空白)
\( (A,\Box)\ (B,\Box)\ (C,\Box)\ (D,\Box)\ (E,\Box) \)
2人目には1番目を除いた4 人が入る。
\( AB, AC, AD, AE, BA, BC \ \cdots EC, ED\)
従って全ての並べ方は
\( 5 \times 4 = 20 \)
通りです。
これの一般式が下式です。
\( \underline{n (n-1) }\)
こんどは5人の中から3選んで並べる仕方はどうなるか。
\( (A,\Box\Box)\ (B,\Box\Box)\ (C,\Box\Box)\ (D,\Box\Box)\ \)
\( (E,\Box\Box) \)
1番目にはA~B の 4 人が入る。
2番目には1番目を除いた4 人が入る。
同様にして、
3番目には1,2番目を除いた3 人が入る。
\( 5 \times 4 \times 3 = 60 \)
通りです。これの一般式が下式です。
\( \underline{ n (n-1)(n-2) } \) です。
以上をまとめると
一般的に「異なる n 個から(重複をゆるさず) r 個を選んで並べる仕方は」
(以下を「エヌ・ピー・アール」などと呼んでいる)
❸:
\( \underline{ {}_{n}P_{r}=n(n-1) \cdots (n-(r-1))} \)
\(\quad \underline{ =\frac{n!}{(n-r)!}} \) ※
通りあります。これを順列といいます。
※
\( ( \because =\frac{n(n-1) \cdots (n-(r-1))(n-r) \cdots 2 \cdot 1}{(n-r)(n-(r+1)) \cdots 2 \cdot 1} ) \)
【注記】
\( {}_{n}P_{n}=\frac{n!}{(n-n)!}=\frac{n!}{0!}=n!\)
\( \quad ( 0!=1 )\)
\( {}_{n}P_{0}=\frac{n!}{(n-0)!}=1\)
5人の名前はA,B,C,D とします。背中にカードを付けています。
\(\fbox{A}\ \fbox{B}\ \fbox{C}\ \fbox{D}\ \fbox{E} \)
結論を先に述べます…
\(
{}_n \mathrm{ C }_r={}_5 \mathrm{ C }_3
=10\)
(※1)通りあります。
次の公式により求めます。
「コンビネーション n, r」などと呼んでいます。
❹:
\(
{}_n \mathrm{ C }_r\)
\(=\frac{{}_{n}P_{r}}{r!}\) \(= \frac{順列}{重複順列} \)
\(=\frac{ n(n-1) \cdots (n-(r-1))}{r!} \)
\( =\frac{n!}{r! \ (n-r)!}\)
(※1):
\(
{}_5 \mathrm{ C }_3 = \frac{{}_{5}P_{3}}{3!}\)
\(=\frac{5\cdot 4\cdot 3}{3\cdot2\cdot1}=10\)
\(r=0\), \(r=n\) のとき:
\({}_n \mathrm{ C }_0 = \)
\(= \frac{ n!}{0!\ (n-0)!}= 1\)
\({}_n \mathrm{ C }_n = \)
\(= \frac{ n!}{n!\ (n-n)!}= 1\)
次のようにも表せる。
右辺を
「2項係数」といい、2項定理の係数です。
❺:
\( \underline {
{}_n \mathrm{ C }_r =\color{red}{ \binom{ n }{ r } } }\)
先に公式を書きましたが、これから 式❹ の導出を行います。
ここで、「3人の中から2人選ぶ組み合わせは何通りか。」をテーマにして進めます。
三人の順序を考慮せず、選ぶ方法を
組み合わせといいます。
例えば{A,B}と{B,A}は同じもので、A,Bからなる集合として扱い\( \{A,B\} \)と表す。
3人から2人選んで並べる仕方は、前記[6]項より
\(_{3}P_{2}=6 \)
通り。
また組み合わせ数は\(3\)通り。
\( \{A,B\} \cdots (A,B) (B,A) \)
\( \{A,C\} \cdots (A,C) (C,A) \)
\( \{B,C\} \cdots (B,C) (C,B) \)
これを次のように分解する
①3人から2人を選ぶ組み合わせの数⇒これを
未知数\(\ x \) とします。
②選んだ2人を1列に並べる仕方⇒\(2!\ \) (前記[5]項の内容です)
[3人から2人を選び、並べる場合の数]\(= [\color{red}{ x }]\times \)[選んだ2人を1列に並べる場合の数]
すなわち:
\(_{3}P_{2}= x \times 2! \)
従って
\( x=\frac{_{3}P_{2}}{2!}\) \(= {}_3 \mathrm{ C }_2=\frac{6}{2}=3\)
上式から「
3人から2人を選ぶ組み合わせの数 \( x \) を」
\(x= {}_3 \mathrm{ C }_2 \)
と表します。
一般に
\(n \) 人から \(r \) 人を選ぶ組み合わせの数は:
\(\underline{ {}_n \mathrm{ C }_r=\frac{_{n}P_{r}}{n!} }\)