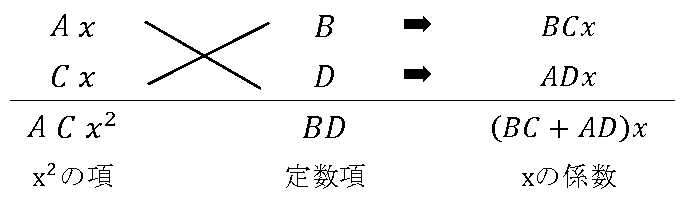
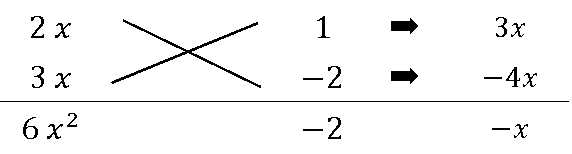\( y=ax^2+bx+c=0 \ \) の解の以下の公式を使う
\( x= \frac{-b \pm \sqrt {b^2-4ac}}{2a} \) … (A)
上の(1)(2)を公式(A)を使って求めてみましょう。
上記(1) \( x^2+3x+2 \)の場合:
公式(A)から \( x=-1, x=-2 \)
∴\( (x+1)(x+2) \)と求まる。
上記(2) \( \ 6x^2-x-2 \)の場合:
公式(A)から \( x=\frac{2}{3}, \ x=-\frac{1}{2} \)
\( (3(x-\frac{2}{3})) 2((x+\frac{1}{2})) \)
∴ \( (3x-2)(2x+1) \) と求まる。
(5)
因数分解できない関数
\(x^2-2x+4\)
2次方程式の解は
\(1 \pm \sqrt-3\) です。
この解は虚数解であり、実数解ではないので因数分解はできません。
この曲線は x軸 との共有点を持たない関数です。
2次方程式の解の公式を使うとき、平方根の中が負の場合は解は求まりません。
3次方程式の解の公式は一般的ではありませんが、あることはありますが、かなり複雑・特殊なので…対象から外します。
5次方程式は存在しません。
(5)
下式を因数定理を使い因数分解する。
\(f(x)=x^3+2^3\)
3次の整式(多項式)の因数分解の
因数定理が活躍します。
(2次の整式の因数分解にも、因数探しに使えますよ!)
【因数定理の参照先】
因数定理の概略:
多項式\(f(x)\)は\(f(a)=0\)となるとき\((x-a)\)の因数をもつ。
すなわち、\(f(a)=0\)なる a を探せば、多項式は\((x-a)\)で割り切れる。
\(f(a)=0\)となる a を探すと \(a=\color{red}{-2}\) である。
これより因数は \((x \color{red}{+ 2})\) である。(
「 2 」の符号に注意)
\(f(x)\) は \((x+2)\) で割り切れる。(因数定理)
以下の割り算をして
【整式の割り算の参考先】
\( \frac{f(x)}{(x+2)}=(x^2-2x+4) \)
\( \therefore x^3+2^3=(x+2)(x^2-2x+4) \)

[コーヒーブレイク/閑話]…お疲れ様でした!
上記の因数分解の式を見ると綺麗な対称性(symmetry)のある式が多いですね!
例えば上の\( x^3+3x^2y+3xy^2+y^3=(x+y)^3 \)は綺麗な対称性の形です。
対称式とはx と yを入れ替えても変わらない式のことです。
幾何学的な対称性、粒子構造の対称性、結晶構造の対称性(雪の結晶)など様々ありますが、自然科学にはまことに綺麗な対称性ものが多いのには驚かせされます。
幾何学の対称性とは物体の形や位置を変えない動かし方(変換)、またはある変換に関して不変である性質。(円、正方形、球など)
新しく発見された素粒子の構造の発見はその対称性から証明されたそうです。