湘南理工学舎,基礎数学,複素数,ド・モアブルの定理,1のn乗根

楽しく学ぶ…基礎数学
ド・モアブルの定理と1のn乗根
( de Moivre's theorem & nth root of 1)
--目　次--

ド・モアブルの定理
複素数と三角関数の式である極形式の複素数の累乗を簡単に求めるための定理です。
次式は絶対値１の複素数\(z=cosθ+i sinθ\)の累乗は絶対値1は変わらず,偏角θ がn 倍するだけである。
これは複素数が複素平面の原点を中心に\(θ\x n\) 分回転することを意味します。

任意の整数\(n\), 任意の実数\(θ\) に対して
\((cosθ+i sinθ)^n=cos\ nθ+i sin\ nθ\) :❶

証　明 (帰納法による)

準備(加法定理):

\(sin(A \pm B)\)\(=sinAcosB \pm cosAsinB \) より
・\(sin(kθ + B)\)\(=sinkθcosB ＋ coskθsinB \)
\(sin(θ+θ)=sinθcosθ+cosθsinθ\)
・\(sin2θ=2sinθcosθ\)

\(cos(A \pm B)\)\(=cosAcosB \mp sinAsinB \) より
・\(cos(kθ + B)\)\(=coskθcosB - sinkθsinB \)
\(cos(θ+θ)\)\(=cosθcosθ +sinθsinθ\)\(=cos^2θ+sin^2θ\)
・\(cos2θ=cos^2θ+sin^2θ\)

以下は帰納法による証明：
\(n\) は任意の整数だから正と負の両方において証明する。

1)n=1 のとき:式①より
\((cosθ+i sinθ)^1=cos1 \cdot θ+i sin1\cdot θ\)
\((cosθ+i sinθ)=cosθ+i sinnθ\)

2)参考→n=2 のとき:式①より
\((cosθ+i sinθ)^2\) \(=cos^2θ-sin^2θ+isinθcosθ\)
加法定理より
\(\therefore (cosθ+i sinθ)^2\)\(=cos2θ+ isin2θ\)

3)\(n=k\) のとき式①が成り立つとして\(n=k+1\) が成り立つか否か。
\(n=k\) のとき:
\((cosθ+i sinθ)^k=cos kθ+i sin kθ\)
\((cosθ+i sinθ)^{k+1}\)\(=(cosθ+i sinθ)^k (cos θ+i sin θ)\) \(=(cos kθ+i sin kθ)(cos θ+i sin θ)\)
\(=coskθ cosθ-sinkθsinθ\) \(+i\ coskθsinθ+i\ sinkθcosθ\)
\(=coskθ cosθ-sinkθsinθ\) \(+i\ (coskθsinθ+sinkθcosθ)\)
\(=cos(kθ+θ)+i\ sin(kθ+θ)\) \(=cos(k+1)θ+i\ sin(k+1)θS\)

以上から帰納法の\(n=1\) のとき成り立ち,\(n=k\) を仮定にして\(n=k+1\)が成り立つことを確認した。

次に\(n=0\) のときの証明

\((cosθ+i sinθ)^n=cosnθ+i sinnθ\)に対し
\((cosθ+i sinθ)^0=1\)
\(cos 0\cdot θ+i sin 0\cdot θ=1\)

∴ 左辺=右辺

最後に\(n\) が負のときの【証明】をします。
すなわち次式となることを証明する。
\(\ul{(cosθ+i sinθ)^{-n}}\)\(\ul{=cos(-nθ)+i sin(-nθ)}\)

【証明】

\((cosθ+i sinθ)^{-n}\) \(=\dsfr{1}{(cos\ nθ+i sin\ nθ)^{n}}\)

分母の共役複素数を掛け分母の実数化する

\(=\dsfr{cos\ nθ-i sin\ nθ}{(cos\ nθ+i sin\ nθ)(cos\ nθ-i sin\ nθ)}\) \(=\dsfr{cosnθ-i sinnθ}{(cos^2nθ+i^2 sin^2nθ)}\) \(=\dsfr{cos\ nθ-i sin\ nθ}{1}\)
\(=cos\ nθ- i sin\ nθ\)

3角関数の特性より
\(cos(-nθ)=cos(nθ)\) \(,\quad -sin(-nθ)=sin\ nθ \)
上式を次のように変形できる

\(=cos(-nθ) + i sin(-nθ)\)

\(\therefore \ul{(cosθ+i sinθ)^{-n}}\)\(\ul{=cos(-nθ) + i sin(-nθ) }\)
…証明終わり…

例題1 次の複素数を計算をしなさい。

\(z^6=(1-i)^6\)

極形式に変換し, ド・モアブルを適用する
\(r=|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\)
\( θ=sin^{-1} \frac{-1}{\sqrt{2}}=-\frac{\pi}{4}\)　(-45° )　
\(z=\sqrt{2}( cos(-\frac{\pi}{4})-i\ sin(-\frac{\pi}{4}) ) \)
\(z^6=\sqrt{2}^6 ( cos(-\frac{\pi}{4}\x 6)\) \(-i\ sin(-\frac{\pi}{4}\x 6) ) \)
\(z^6=2^3 [cos(-\frac{3}{2}\pi)-i\ sin(-\frac{3}{2}\pi) ] \)

例題2 次の複素数を計算をしなさい。

\(z^5=[cos(\frac{\pi}{3}) +i sin (\frac{\pi}{3})]^5 \)

\(z^5=cos(\frac{5 \pi}{3}) +i sin (\frac{5 \pi}{3})\)

この偏差角は第4象限だから　\(θ=\frac{5 \pi}{3}-2\pi\)\(=-\frac{\pi}{3}\)
\(cos(2\pi-θ)=cosθ,\ sin(2\pi-θ)=-sinθ \)

\(=cos(-\frac{\pi}{3}) +i sin (-\frac{ \pi}{3})\)
\(=\frac{1}{2}-\frac{\sqrt{3}}{2}\)

例題3 次の複素数を計算をしなさい。

\(z^4=[\frac{\sqrt{2}}{2} +i (\frac{\sqrt{6}}{2})]^4 \)

\(z=\sqrt{2}[(\frac{1}{2}) +i (\frac{\sqrt{3}}{2}) ] \)

\(\sqrt{2}\) でくくるのがポイント
以下にして極形式に変換できる

\( =\sqrt{2}[cos(\frac{\pi}{3})+i\ sin(\frac{\pi}{3}) ]\)

同じcosとsinの偏角\(θ=\frac{\pi}{3}\) が導き出せた
式❶が使える

\(z^4=(\sqrt{2})^4\ \underbrace{ [cos(\frac{\pi}{3}) +i sin (\frac{\pi}{3}) ]^4 }_{公式❶により}\)
\(=4\ [cos(\frac{4 \pi}{3}) +i sin (\frac{4 \pi}{3}) ]\)

\(cos(\frac{4 \pi}{3})=cos(\pi+\frac{1 \pi}{3})\) \(=-cos(\pi+\frac{1 \pi}{3})\)
\(sin(\frac{4 \pi}{3})=sin(\pi+\frac{1 \pi}{3})\) \(=-sin(\pi+\frac{1 \pi}{3})\)

\(=4\ [-cos(\frac{\pi}{3}) -i sin (\frac{\pi}{3}) ]\) \(=4\ [-\frac{1}{2} -i \frac{\sqrt{3}}{2}]\) \(=-2 -i 2 \sqrt{3}\)
\(=2(-1 -i \sqrt{3})\)

例題4 次の複素数を計算をしなさい。

\(z^6=(1-i)^6\)

極形式に変換し, ド・モアブルを適用する
\(r=|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\)
\( θ=sin^{-1} \frac{-1}{\sqrt{2}}=-\frac{\pi}{4}\)　(-45° )　
\(z=\sqrt{2} \underbrace{ ( cos(-\frac{\pi}{4})-i\ sin(-\frac{\pi}{4}) )}_{定理を適用} \)
\(z^6\small{=\sqrt{2}^6\ ( cos(-\frac{\pi}{4}\x 6)-i\ sin(-\frac{\pi}{4}\x 6) ) } \)
\(=2^3\ [cos(-\frac{3}{2}\pi)-i\ sin(-\frac{3}{2}\pi) ] \)
\(=8 [cos(2\pi-\frac{3}{2}\pi)-i\ sin(2\pi-\frac{3}{2}\pi) ] \)
\(=8 [cos(\frac{\pi}{2})-i\ sin(\frac{\pi}{2})] \) \(=8 [0-i\ 1] \)\(=-8i\)

fig1 \(z^2\)～\(z^6\)

1 のｎ乗根

複素数Zの方程式 \(Z^n =1\) (n乗して1になる) の解を 1のｎ乗根 という。
\(z\) の1 のｎ乗根とは
\(z=|z|(cosθ+i sinθ)=1\) の\(|z|\)は 1 であるから (※1)
\(z=(cosθ+i sinθ)=1\)　(※2) といえる。

(※1)\(z^n=1\) から \(|z^n|=|1|\), \(\ |1|=1\)は自明
\(|z^n|=|z|^n=1　\to \) \(\therefore　\ul{ |z|=1 }\) \(\quad (|z|\ge 0) \)

式(※2)式はド・モアブルの定理が使えて,次式が成り立つ:
\(z=(cosθ+i sinθ)=1\)　:ⓐ\(\quad (0\le θ \lt 2\pi)\)
\(z^n=(cosnθ+i sinnθ)=1\)　:ⓑ \(\quad (0\le nθ \lt n2\pi)\)

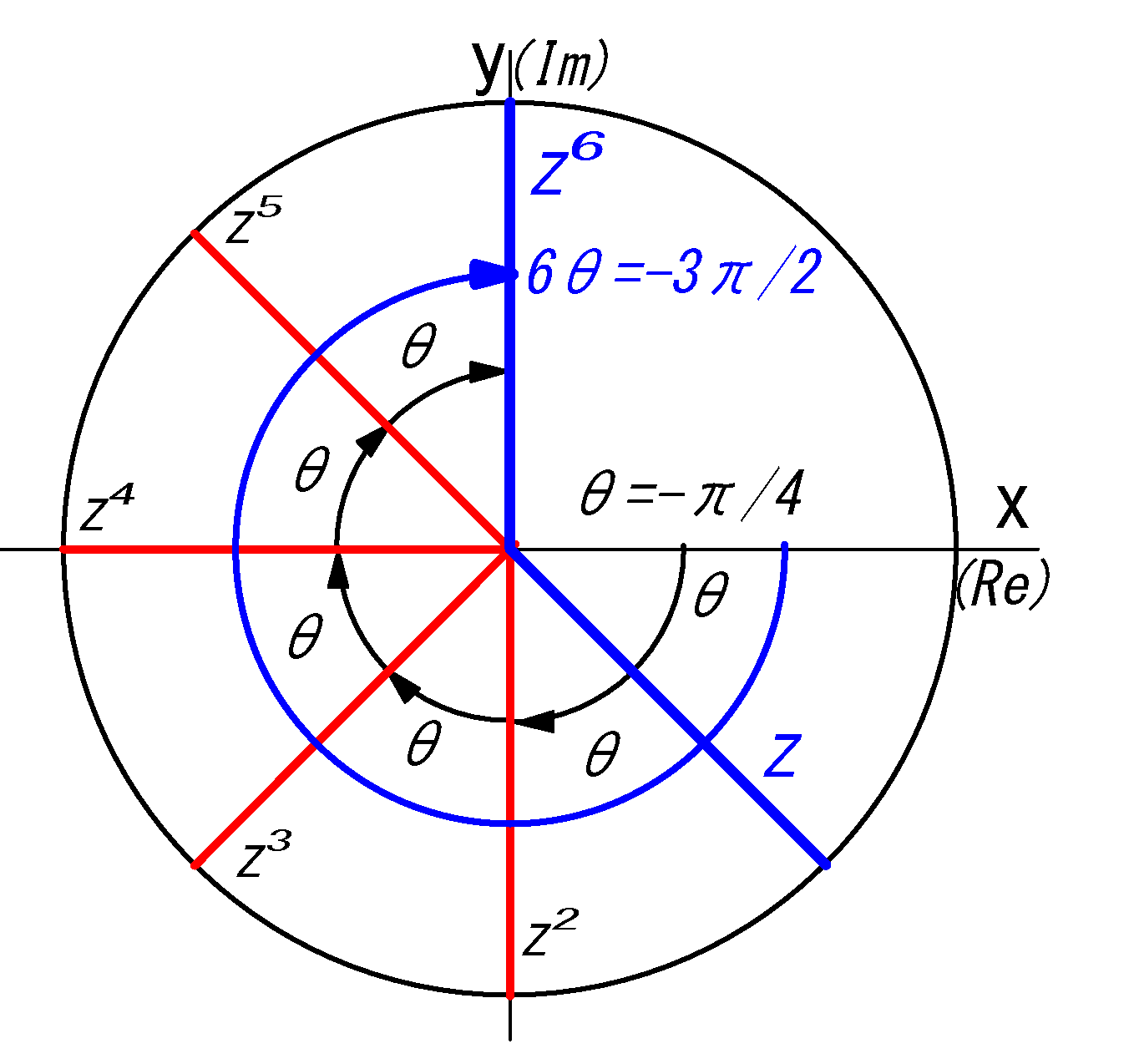
例題5 \(z^4=1\)の解を求めよ

\(z^4=(cos4θ+i sin4θ)=1\) \((0\le 4θ \lt 8\pi)\)
上式を満たす実部,虚部は:
実部:\(cos4θ=1\),　虚部:\(sin4θ=0\) であり, その偏角\(4θ\) は
\(4θ=0\) を起点に \(\cdots\) \(\cdots\)\(2\pi,4\pi,6\pi\)である。(\(8\pi\)は定義域をオーバする）
\(\ul{θ=0,\ \dsfr{\pi}{2},\ \pi,\ \dsfr{3\pi}{2}}\) ← (\(0,\ \frac{2\pi}{4},\ \frac{4\pi}{4},\ \frac{6\pi}{4}\) )
を式ⓐの\(\small{z=(cosθ+i sinθ)=1}\) に代入し

\(z_0=(cos0+i sin)=1+0=1\)
\(z_1=(cos\frac{\pi}{2}+i\ sin\frac{\pi}{2})=0+i=i\)
\(z_2=(cos\ \pi+i\ sin\ \pi=-1+0=-1\)
\(z_3=(cos\frac{3\pi}{2}+i\ sin\frac{3\pi}{2})=0-i=-i\)

\(z_0=1\) \(,\ z_1=i\) \(,\ z_2=-1\) \(,\ z_3=-i\)
…解答終わり

この例題での \(z_0\)~\(z_3\)の各偏角を考察してみると:
\(n=4\)が指定され, \((0\le 4θ \lt 8\pi)\)
\(k=n-1\)とおくと \(4θ_k=2k\pi\) となり
\(\therefore θ_k=\frac{2k}{4}\pi\)

\(θ_0=\frac{2\cdot 0}{4}\pi=0\) \(,\quad θ_1=\frac{2\cdot 1}{4}\pi=\frac{1}{2}\pi\)
\(θ_2=\frac{2\cdot 2}{4}\pi=\pi\)\(,\quad θ_3=\frac{2\cdot 3}{4}\pi=\frac{3}{2}\pi\)

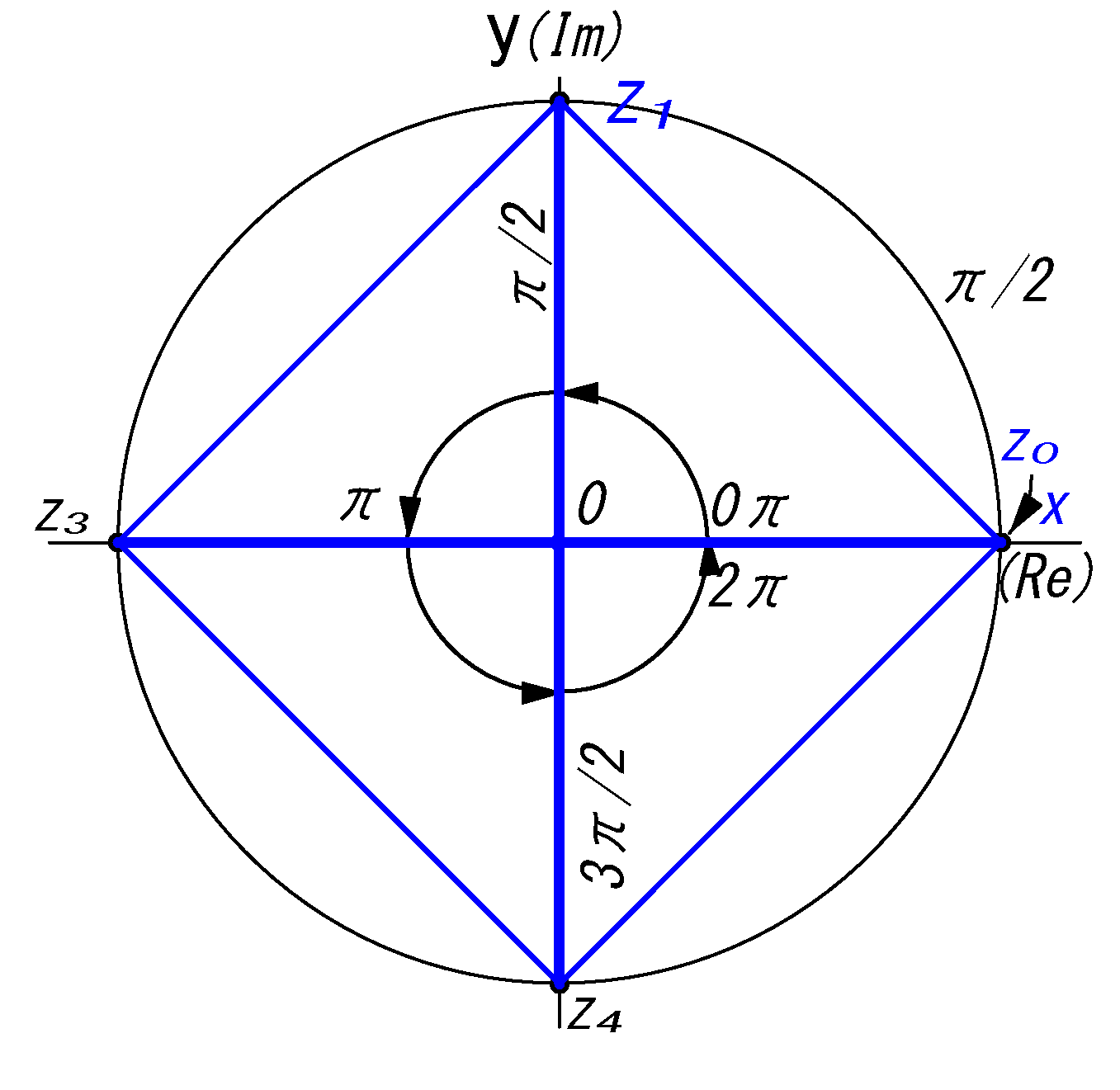
fig2/ 1の4乗根 \(z^4 =1\)

各偏角\(\ \ul{n\ θ_k}\ \) を一般化すると
\(n\) に対し\(k=1,2 \cdots n-1\) とすると
\(n\ θ_k=2k\pi\) \(,\quad θ_k=\frac{2k}{n}\pi\)
となる。

ここで「1 のｎ乗根」について一般式と性質にまとめるみる。
1 のｎ乗根の式

自然数n に対し1 のｎ乗根(解)は次式の複素数である。
k はnに対し \(k=0,1,2 \cdots,n-1\)である
\(z_k=cos \dsfr{2k\pi}{n}+i\ sin \dsfr{2k\pi}{n}\) :➋

式❷の証明

方程式 \(z^n-1=0\)より \(|z^n|=|1|\), \(\ |1|=1\)
\(|z^n|=|z|^n=1　\to \) \(\therefore　\ul{ |z|=1 }\) \(\quad (|z|\ge 0) \)
\(z=cosθ+i\ sin θ\) とおくと
ド・モアブルの定理の定理より
\(z^n=(cosθ+i\ sin θ)^n\) \(=(cosnθ+i\ sin nθ)\) であり,また
\(cosnθ+i\ sin nθ=1\) だから、実部と虚部を注目すると
\(cosnθ=1\)\(\quad, sin nθ=0\)
\(θ=0,2\pi,4\pi \cdots \)とおけば成立するね
\(n\ θ\) は\(2\pi\) の整数倍となる。ここで\(n\) に対し次の係数を用意する
\(k=1,2,\cdots n-2,n-1\) \(ｋ\) は自然数\(n\) より1小さい整数
式の一般化のための次の関係式ができる:
\(n\ θ_k=2k\pi\) \(,\quad θ_k=\frac{2k}{n}\pi\)
\(z^n \to z^k\) として次式が書ける
\(z_k=cos\ θ_k + i \sin\ θ_k\)
これより
\(z_k=cos \dsfr{2k\pi}{n}+i\ sin \dsfr{2k\pi}{n}\) :➋

1 のｎ乗根の性質

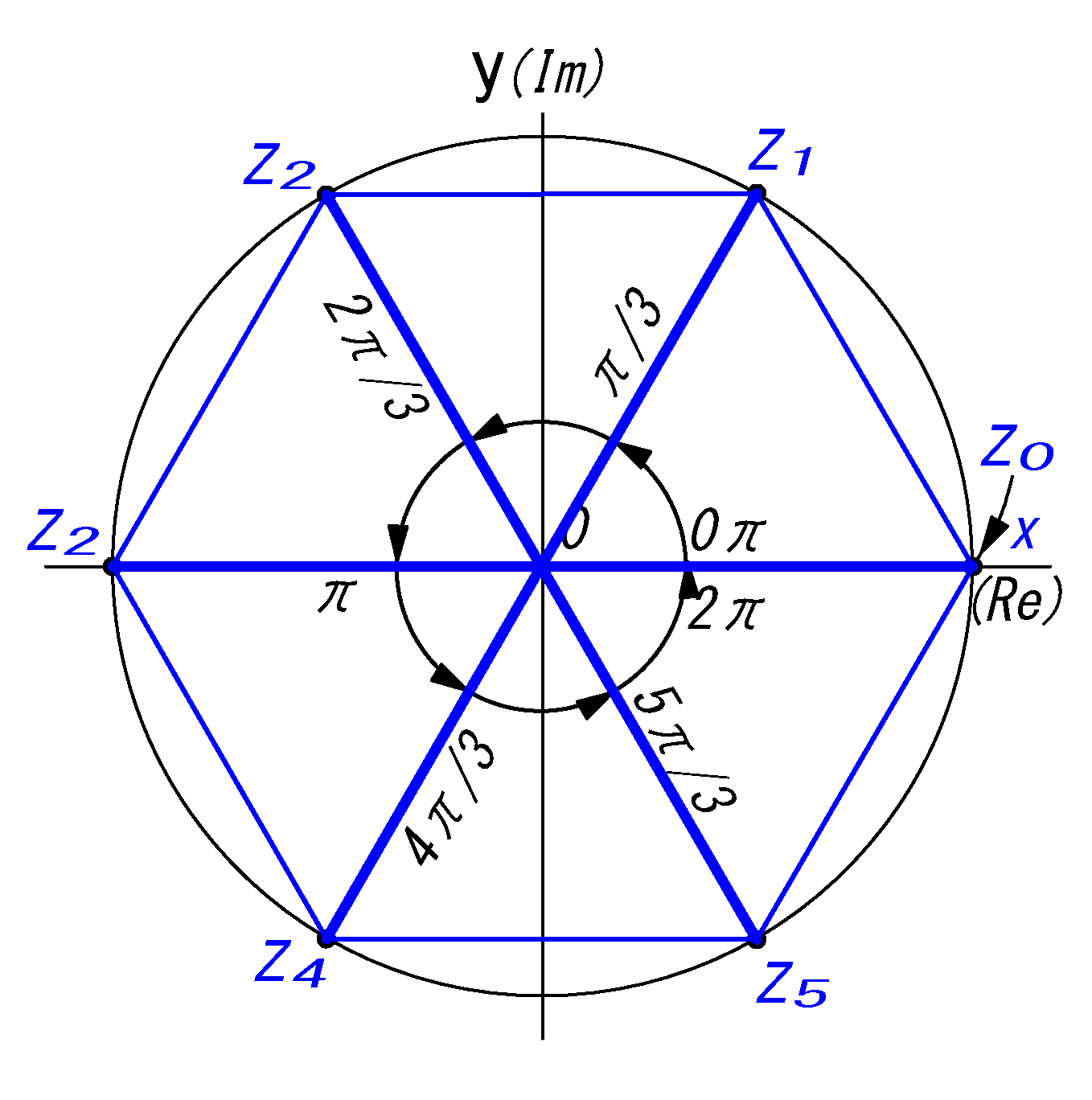
1)\(z_k\)が示す点は単位円をn 等分する分点である。
(単位円周上に等間隔にある。)
2)特に\(n\ge 3\) のときは\(z_k\)が示す点を頂点として, 単位円に内接する正n 角形の頂点となる。
(正三角形(\(z^3\))から正n 角形(\(z^n\))の頂点が描ける)
3)1のn乗根はn 個ある。
4)1のn乗根の和は0 である。

例題6 \(z^6=1\)を解いて, fig2を参考に作図せよ。

式❷を使い解いていく:

\( θ_k=\frac{2k}{n}\pi\)
\(z_k=cos \dsfr{2k\pi}{n}+i\ sin \dsfr{2k\pi}{n}\) ➋

各偏角を求める

\( θ_0=\frac{0}{6}\pi=0\) \(,\quad θ_1=\frac{2\cdot 1}{6}\pi=\frac{1}{3}\pi\) \(,\quad θ_2=\frac{2\cdot 2}{6}\pi=\frac{2}{3}\pi\) \(,\quad θ_3=\frac{2\cdot 3}{6}\pi=\pi\) \(,\quad θ_4=\frac{2\cdot 4}{6}\pi=\frac{4}{3}\pi\) \(,\quad θ_5=\frac{2\cdot 5}{6}\pi=\frac{5}{3}\pi\)
\(θ_6=\frac{2\cdot 6}{6}\pi=\xcancel{2\pi }\) 領域外 \((0\le θ \lt 2\pi)\)

\(θ_0\to θ_5\) を式❷ に代入し, 解を求めていく
\(z_0=cos\ 0 + i \sin\ 0＝1\)
\(z_1=cos\ \frac{\pi}{3} + i \sin\ \frac{\pi}{3}\) \(=\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
\(z_2=cos\ \frac{2\pi}{3} + i \sin\ \frac{2\pi}{3}\) \(=-\frac{1}{2}+\frac{\sqrt{3}}{2}i \)
\(z_3=cos\ \pi + i \sin\ \pi\) \(=-1\)
\(z_4=cos\ \frac{4\pi}{3} + i \sin\ \frac{2\pi}{3}\) \(=-\frac{1}{2}-\frac{\sqrt{3}}{2}i \)
\(z_5=cos\ \frac{5\pi}{3} + i \sin\ \frac{5\pi}{3}\) \(=\frac{1}{2}-\frac{\sqrt{3}}{2}i \)
下図の通り \(z_0\to z_5\)の点を結べば, 単位円に内接する正六角形が描ける。

fig3/ 1の6乗根 \(z^6 =1\)

…以上

coffe

[コーヒーブレイク/閑話］…お疲れさまでした