[コーヒーブレイク/閑話]…お疲れ様でした!
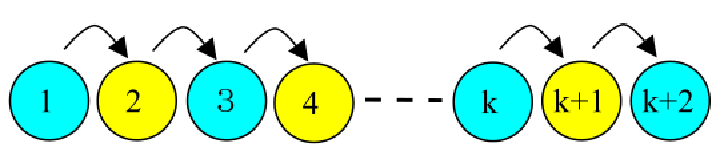
帰納法は数学以外(哲学など)でも使うので、私たちは数学的帰納法と明記しましょう。(上でははじめに注記してます)初めての方は「数学的帰納法で本当の証明になるのか?」「背理法にいたっては、もっと疑問がわく」などと悩む方もいるかと思いますが、 これは慣れるまで素直に受け入れることが肝要です。
受け入れて先に進みましょう。(人生は有限です…先にはまだ学ぶことが沢山待っています) 帰納法に対して演繹法(えんえき)(reduction)がありますが、数学的演繹法は聞いたことはありません、演繹法とは超簡単に言うと「A=B、B=C なら A=C」が言えるような、 誰でも同じ結論となる推論のことで、数学自体が演繹法なのです…ということです。