湘南理工学舎・初歩の数学・指数法則と累乗根

楽しく学ぶ…基礎数学
指数法則と累乗根
(power law & power root)
--目　次--

♦指数法則について
♦実数の指数法則
♦例題(指数)
♦累乗根について
♦補足説明(累乗根)
♦\(n\)累乗根\(a\)とは
♦累乗根の公式
♦累乗根の公式の導出
♦例題(累乗根・指数)

指数法則について

ある数\(a\) を\(n\) 回掛け合わたのものを\(\st{a^n}\) と表す。
\(\st{n}\)を指数と言う。(掛算の回数)
また累乗とは同じ数をいくつかかけ合わせる計算である。
\(\st{a^n}\) を\(\st{a}\)のｎ乗と言う。
\( a \x a=a^2\)
\( a \x a=a^3\)

\( \underbrace{a\x a\x \cdots \x a}_{n 個} =a^n\)
指数\(n\)は自然数からはじまり次のように拡張されていく。
自然数→整数→有理数→実数
注: \(a^n\) の\(n\) が実数, 複素数まで拡張する時の用語は累乗でなく冪乗(べき乗)を使うことがあるが,ここでは累乗を使います。

【補足】指数関数
　\(\st{ｙ=a^x}\)の式を指数関数という。
　\(x\):指数　 \(a\):底という。

実数の指数法則

\(a\gt 0, \ b\gt 0\) \(r,s\)は実数とする。
❶ \(a^r a^s=a^{r+s}\) \(\ , \ \) \(\dsfr{a^r}{a^s}=a^{r-s}\)
❷ \((a^r)^s=a^{rs}\)
❸ \((ab)^r=a^r b^r\) \(\ , \ \) \((\dsfr{a}{b})^r=\dsfr {a^r}{b^r} \)

注:❶の右式は指数が負の時の分数表示。
例えば\(a^ra^{-s}=\dsfr{a^r}{a^s}\)

また次の式が成り立ちます。
❹ \(a^0=1\) \(\ , \ \) \(a^{-1}=\dsfr{1}{a}\)
初めてこの式を見ると次の疑問を浮かべるのではないか？
・数a を0回掛けると何故 1 になるのか?
・数a を-1回掛けると何故 1/a になるのか?
何故ならば:

\(\frac{a^r}{a^r}=1\) \(\ , \ \) \(\frac{a^r}{a^r}=a^{r-r}=a^0\)
\(\therefore \ul{a^0=1}\)

\(s=-r\) とすると \(a^r a^s=a^{r-r}=a^0\)
\(a^r a^{-r}=1\) \( \to a^{-r}=\frac{1}{a^r}\)
r=1 とすると
\(\therefore \ul{a^{-1}=\frac{1}{a} } \)

例題指数

1) \((a^{-2})^2=a^{-4}=\frac{1}{a^4}\)

2) \((a^2 b^{-2})^{-2}=(a^2)^{-2}(b^{-2})^{-2}\)\(=a^{-4} b^{4}\)\(=\frac{b^4}{a^4}\)

3) \(a\x a^2=a^{1+2}=a^3\)

4) \(b\x b^{-3}=b^{1-3}=a^{-2}=\frac{1}{a^2}\)

5) \((a^{\frac{1}{r}})^{\frac{1}{s}}\)\(=(a^{\frac{1}{rs}})\)

6) \( (a^{ \frac{1}{r} })^{r}=a\)

7) \(2^2\x 2^5 ÷ 2^4\)\(=2^{2+5} ÷ 2^4\)\(=\frac{2^7}{2^4}=2^{7-4}=2^{3}=8\)

8) \(\dsfr{4^5}{8^2}=\frac{(2^2)^5}{(2^3)^2}\)\(=\frac{2^{10}}{2^{6}}\) \(=2^{4}=16\)

9) \(8^{\frac{1}{3}}\) \(=\sqrt[ 3 ]{8}\)\(=\sqrt[ 3 ]{2^3}\)\(=2\)

10) \((-4)^{-2}=\frac{1}{(-4)^2}\)\(=\frac{1}{16}\)

11) \( (0.5)^{-3}=(\frac{1}{2})^{-3}\)\(=\frac{1}{(\frac{1}{2})^{3}}\) \(=(\frac{2}{1})^{3}\)\(=2^3=8 \)

12) \(\sqrt{0.01}=\sqrt{0.1\x 0.1}\)\(=\sqrt[2]{(0.1)^{2}}=0.1\)

累乗根について

n は正の整数, a は実数として, n 乗してaになるような数をa のn乗根 または累乗根と言う。
\(\quad \sqrt[n]{a} \) と表す。

ここでは\(a=x^n\) である。
a のn乗根 とは \(a=x^n\) の解のことである。

次のときは,独自の呼び方があります。
\(\sqrt[2]{a}\): 平方根といい, また \(\sqrt{a}\)　と表す。
\(\sqrt[3]{a}\): 立方根という

\(\st{\sqrt[n]{a}} \) の定義

(1) n が奇数のとき a の n乗根は1つだけ存在し,\(\sqrt[n]{a} \)と表す。
(2) n が偶数のときａ(a>0) の n乗根は2つ存在し,これを「正を\(\sqrt[n]{a} \) 」, 「負を\(-\sqrt[n]{a} \) 」と表す。
また a が負の n乗根は存在しない。(∵偶数乗して負になる実数はない)
(3) \(\sqrt[n]{0}=0 \)

fig1 累乗とグラフ

補足説明 nbsp;累乗根
幾つかの具体例を見ていきましょう。
一般に「a の n乗根」(\(a\ne o\))の解はｎ個あります。
a はここでは実数を扱いますが,参考として以下は複素数も扱ってみます。

•4 の2乗根は+2 , -2 の2つ

∵ \(x^2=4 \to x^2-4=0\) \(\to (x-2)(x+2)=0\)
(2乗根4\(=\sqrt{4}=2\))
(2乗根-4\(=-\sqrt{4}=-2\))

•27 の3乗根は3の1個(実数解)
複素数を含めると\(\frac{-1+\sqrt{3}i}{2}\), \(\frac{-1-\sqrt{3}i}{2}\) の3つ

∵ \(x^3=27 \to x^3-27=0\)\(\to (x-1)\ul{(x^2+x+1)}=0\)
\(x=\frac{-1\pm \sqrt{1-4\cdot1}}{2}\) \(=\frac{-1\pm \sqrt{-3}}{2}\) \(=\frac{-1\pm \sqrt{3} i}{2}\)
(3乗根27\(=\sqrt[3]{27}=3\) )

•8 の3乗根は2 の1つである。(実数解)
但し,上記同様に複素数を含めれば3つである。

\(x=-1+\sqrt{3}i\)　\(,\ -1+\sqrt{3}i\)
(3乗根8\(=\sqrt[3]{8}=2\) )

… \(\downarrow\) ここからは実数解を扱います \(\downarrow\) …

上記ように「a のn乗根」と以下の「\(n\)乗根\(a\)」とは答える内容が違うので注意する。
これからの例題では「\(n\)乗根\(a\)」を求めることが主体です。
\(n\)乗根\(a\) とは

先に述べたように実数解において「a のn 乗根」nが偶数なら2つ、奇数なら1つです。
しかし,「n 乗根a」のときは1つです。
(以下の公式,例題では「n 乗根a」です)
n 乗根a とは\(\ul{\sqrt[n]{a}}\)のことで答えは1つ。
答えが\(x\) なら解答は \(\sqrt[n]{a}=x\) で完了する。

• n乗根a\(=\sqrt[n]{a}=\pm x\)　:間違い
• (2乗根-4)\(=\sqrt{-4}\)　:間違い (2乗して負になる実数はない)
• 3乗根8\(=\sqrt[3]{8}=2\)
• 3乗根- 8\(=\sqrt[3]{-8}=-2\)Ⓐ
• 2乗根4\(=\sqrt{4}=2\)
• - (2乗根4)\(=-\sqrt{4}=-2\)Ⓑ　「マイナス2乗根4と呼ぶ」
ⒶとⒷを混乱しないように注意

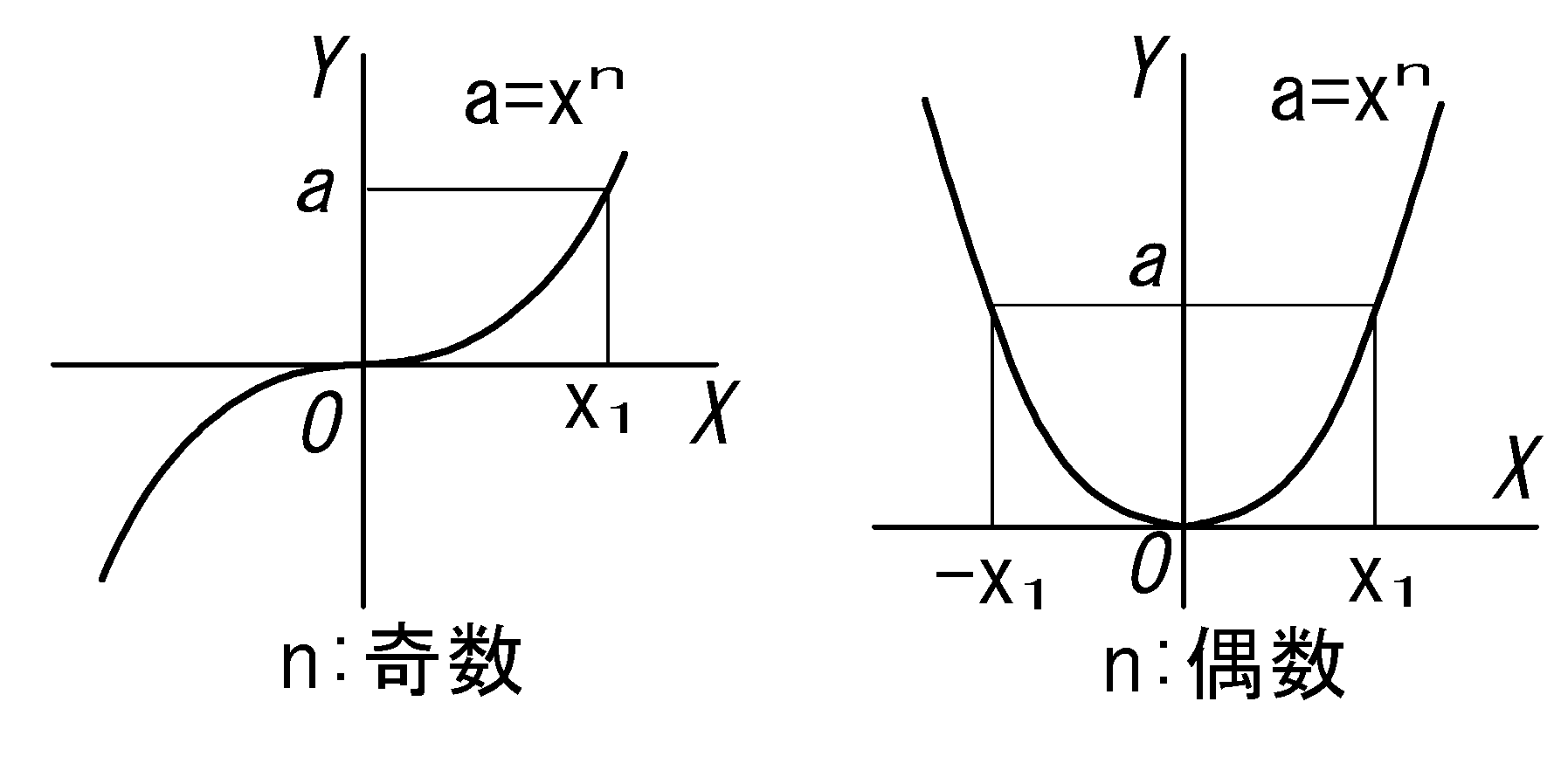
次の累乗根の公式において、条件の \(a \gt 0\), \(\ b \gt 0\) から指数n の偶数/奇数にかかわらず累乗根の結果は正の数であることに注意。

累乗根の公式 (累乗根の性質ともいう)

\(a \gt 0\), \(\ b \gt 0\) とし, m, n, p は正の整数とするとき次式が成り立つ。
❶ \(\sqrt[n]{a}\ \sqrt[n]{b }=\sqrt[n]{a\ b }\)

❷ \(\dsfr{\sqrt[n]{a}}{\ \sqrt[n]{b}}=\sqrt[n]{ \dsfr{a}{b} }\)
❸ \( (\sqrt[n]{a})^m=\sqrt[n]{a^m} \)

❹ \( \sqrt[m]{ \sqrt[n]{a} } =\sqrt[m\ n]{a} \)

❺ \( \sqrt[n]{a^m} =\sqrt[p\ n]{a^{p\ m}} \)

累乗根を指数で表すと:
❻ \( \sqrt[n]{a}=a^{\frac{1}{n}}\)

\(\therefore (\sqrt[n]{a})^{n}=a\)\(,\ \) \((a^{\frac{1}{n}})^{n}=a\)

累乗根の公式の導出

❶ \(\sqrt[n]{a}\ \sqrt[n]{b }=\sqrt[n]{a\ b }\)
左辺と右辺をn乗する:
\(\ul{ (\sqrt[n]{a}\ \sqrt[n]{b})^n}=(\sqrt[n]{a})^n\ (\sqrt[n]{b})^n\) \(=ab\)
\(\ul{(\sqrt[n]{a\ b })^n}=ab\)
下線部(公式をn乗)どうしが等しいから
\(\therefore \sqrt[n]{a}\ \sqrt[n]{b }=\sqrt[n]{a\ b }\)

❷ \(\dsfr{\sqrt[n]{a}}{\ \sqrt[n]{b}}=\sqrt[n]{ \dsfr{a}{b} }\)
左辺と右辺をn乗する:
\( \ul{ \left(\dsfr {\sqrt[n]{a}} {\sqrt[n]{b}} \right)^n }\) \(= \dsfr{ (\sqrt[n]{a})^n}{ (\sqrt[n]{b})^n } \) \( =\dsfr{a}{b}\)
\( \ul{\left(\sqrt[n]{ \dsfr{a}{b} }\right)^n }\)\( =\dsfr{a}{b}\)
下線部(公式をn乗)どうしが等しいから:
\(\therefore \dsfr{\sqrt[n]{a}}{\ \sqrt[n]{b}}=\sqrt[n]{ \dsfr{a}{b} }\)

❸ \( (\sqrt[n]{a})^m=\sqrt[n]{a^m} \)
左辺をn乗すると
\( \left(\ \ul{ (\sqrt[n]{a}\ \ )^m}\ \right)^n\) \(= \left( (\sqrt[n]{a}\ )^n \right)^m=a^m\)
下線部のn乗根をとると公式❸を得る
\(\therefore (\sqrt[n]{a})^m=\sqrt[n]{a^m} \)

❹ \( \sqrt[m]{ \sqrt[n]{a} } =\sqrt[m\ n]{a} \)
左辺をmn乗すると
\( \left(\sqrt[m]{ \sqrt[n]{a} } \right)^{mn}\) \(= \left( ( \sqrt[m]{ \sqrt[n]{a\ } }\ )^m \right)^{n}\) \(= \left( ( \sqrt[n]{a\ } \right)^{n}\)\(=a\)
ここでa のmn乗根を考えると, 上記の結果より:
\(\therefore \sqrt[m]{ \sqrt[n]{a} } =\sqrt[m\ n]{a} \)

❺ \( \sqrt[n]{a^m} =\sqrt[p\ n]{a^{p\ m}} \)
左辺をnp 乗すると:
\( \ul{ (\sqrt[n]{a^m} )\ ^{np}}\)\(=\left((\sqrt[n]{a^m})^{n} \right)^{p}\) \(=a^{mp}\)\(=\ul{a^{pm}}\)
さらに\(a^{pm}\)のnp乗根　\(\to \sqrt[p\ n]{a^{p\ m}} \)
以上は左辺をnp乗後,さらにnp乗根して式変更すると公式の右辺になった。
\(\therefore \sqrt[n]{a^m} =\sqrt[p\ n]{a^{p\ m}} \)

例題累乗根,指数

以下の1)～5)は累乗根公式❶～❺の応用
1) \(\sqrt[3]{3}\ \sqrt[3]{9}=\sqrt[3]{27}\)\(=\sqrt[3]{3^3}=3\)

2) \(\dsfr{ \sqrt[3]{25} }{ \sqrt[3]{5} }\)\(=\sqrt[3]{\dsfr{25}{5}}=\sqrt[3]{5}\)

3) \( (\sqrt[4]{36})^2=\sqrt[4]{36^2}=\sqrt[4]{(6^2)^2}\)\(=\sqrt[4]{6^4}=6\)

4) \( \sqrt[3]{4}\ \sqrt[3]{128}= \sqrt[3]{4}\ \sqrt[3]{2\x 64}\) \(=\sqrt[3]{4}\ \sqrt[3]{2}\ \sqrt[3]{64} =\sqrt[3]{8}\ \sqrt[3]{64}\) \(=2 \x 4=8\)

5) \( \sqrt[8]{2^{12}}\) \(=\underbrace{\sqrt[2\x4]{2^{3\x4}}=\sqrt[2]{2^{3}} }_{公式❺}\) \(=\sqrt{2^{3}}\)\(=(\sqrt{2})^3=2\sqrt{2}\)

6) \( \sqrt[3]{216}\) \(=\sqrt[3]{2\x 2\x 2\x 3\x 3\x 3\x 3\ } \) \(=\sqrt[3]{2^3 \x 3^3\ }\)\(=\sqrt[3]{6^3\ }\)\(=6\)
216を素因数分解した。

7) \(\sqrt[6]{8}\) と \(\sqrt[3]{4}\) の大小を求めよ。
(底を同じにして,指数を比較する方法)
\(\sqrt[6]{8}=\sqrt[6]{2^3}\) \(=2^{\frac{3}{6}}\)\(=2^{\frac{1}{2}}\)
\(\sqrt[3]{4}=\sqrt[3]{2^{2}}\) \(=2^{\frac{2}{3}}\)
指数の大小は \(\frac{1}{2} \lt \frac{2}{3}\)だから:
\(\sqrt[6]{8}\) \(\lt\) \(\sqrt[3]{4}\)

8) \((\sqrt[3]{8})^{20}\) と \((\sqrt{81})^5\)の大小を求めよ。
(指数を同じにして,底を比較する方法)
\((\sqrt[3]{8})^{20}\)\(=2^{20}\)\(=2^{2\x10}\)\(=4^{10}\)
\((\sqrt{81})^5=9^{5}\)\(=(3^2)^5=3^{10}\)
底の大小は\(　4 \gt 3\)　
\( (\sqrt[3]{8})^{20} \gt (\sqrt{81})^5 \)

・・・以上

coffe

[コーヒーブレイク/閑話］…お疲れさまでした