各種平均

 学校のある学年にクラス数が n 個 あり、各クラスの人数が \( a_1, a_2, \cdots ,a_n \)
このとき平均クラス人数 \(N_a\):

\(N_a= \frac{a_1+ a_2+ \cdots +a_n }{n}\) である。

---

 関連する n 個の比率データ数などの平均は以下の相乗平均の式を使います。

\(N_g= \sqrt[n]{a_1+ a_2+ \cdots +a_n }\)

【応用例】
前年度比率から４年後の学生人を求める
下表はある学校の学生人数の統計データです。
得ているデータは：
・基準は2015年の700人
・前年度比率
・人数（実データ）は未知です。（ここでは説明のため記載している）

上の条件で4年後の年学生人数を求める

注(※1)；前年度比率 ☜ キーポイント

①４年間の前年度比率から相乗平均を求める。
②求めた相乗平均を使い、「2015年の700人」のデータから4年後の2019年の人数を算出する。

参考に相和平均も載せておきました…比較して下さい。
相和平均では合わないことが判ります。

相乗平均：
 \(H_g=\sqrt[4]{1.142\times1.125\times0.778\times0.857} \) 　
 \(=0.96219\) …4年後の人数が実データと合致する。

相加平均：（参考）
 \(H_a=\frac{1.142+1.125+0.778+0.857}{4}\) 　
 \(=0.9757\)　 …4年後の人数が実データから外れる。

 基準の700人に平均値を掛けて❶と❷を埋めたのが下表。
（例：\(700 \times 0.96219=673.5\)   \(700 \times 0.9757=682.99\)）
【答え】は「599.9⇒600人」です。

わざと計算結果のまま「599.9」としておきましたが 「600人」です。相乗平均を使うのが適格です。

以上は説明のための計算でした。
通常は次のように簡単に早く計算できます。
相乗平均　\(k=0.96219\) として
４年後の学生数は:
 \( (((700\times k) \times k ) \times k)\times k \) \(\underline{=700 \times k^4} \)
\(=700 \times 0.8571\)　\(=599.9\)
簡単で計算できました。

相乗平均の応用として 前年度の人口比率、売上比率、利回りなどに使われます。

---

　　

複利とは: 初期の元本 100 万円、金利 5 % として 貯金、１年後 は利子5 万円、これを加えて 105 万円となる。
この105 万円 を 元本にして再び 貯金（または投資）して その1年後は 利子5.25万円となり 合計 110.25 万円となる。
このようにして３年後には 151.8 万円になる。…❶　
下記でこの金額を「年平均の利回り」を使い算出します。 このように 複利は元本が毎年更新される。
複利に対して「単利」というが、単利は利子を元本に入れない。

例えば、利回りが３年前 10%、２年前 15%、１年前 20% でした。
この過去３年間の「平均利回り」は以下の幾何平均で求めます。
\( \sqrt [3]{1.1 \times 1.15 \times 1.2} =1.14927\)
年平均の利回りは 14.927 %　となりました。
この数値を使い３年後の貯蓄額を求めます。
 \( \color{red}{k}=1+0.14927=1.14927\)
３年後の貯蓄額:
 \( ((100\times k) \times k ) \times k) \) \(=100 \times \color{red}{k^3})\)

\(=151.8\) 万円　…❷　
∴　❶=❷

---

　　　　

長方形の面積(2辺 \(b, c\))は\( S=b c\) です。
\(S\) の平方根は\( \sqrt{S}=\sqrt {b\ c}=a \)…この意味は！
これは長方形の辺を平均化して正方形を作ったことになります。
\( S=a^2=\sqrt {b\ c} \times \sqrt {b\ c}　\)

直方体の体積\( V= b \times c \times d \) も同様です。
\( V=a^3= \sqrt[3]{b\ c\ d} \times \sqrt[3]{b\ c\ d} \times \sqrt[3]{b\ c\ d} \)
直方体の各辺を平均化して立方体（正6面体）の辺の長さ \(a\) を求めたことになります。

相加平均と相乗平均の関係式（(1)と(1)'）を「相加相乗平均の不等式」という。
条件: \(a >0,　\ b>0\)
下式が成り立ちます。
\( \underline{ \ \ \frac{a+b}{2} \ ≥\sqrt {a b} }\qquad (1)\)
（相加平均 ≥ 相乗平均）

【式(1)の証明】

\( a+b-2\sqrt{ab}=(\sqrt{a}-\sqrt{b})^2 \ge 0\)
\(a+b-2\sqrt{ab} \ge 0\)
\(\therefore \frac{a+b}{2} \ge \sqrt{ab}\)

\( a=b \) のとき、等号が成立する。
等号が何を意味するか⇒左辺が最小値である。
したがって、\(\frac{a+b}{2}\) は最小値であり、最小値は右辺の \(\sqrt{ab}\) である。

式を変形すると、よく使う式になる。
\( \underline{a+b ≥2\sqrt {a b} }\qquad (1)'\)

---

式(1)' を用いて
\( x+\frac{8}{x} ≥ 2 \sqrt{x \cdot \frac{8}{x}} \ \)

公式に対し\(a=x, \ b=\frac{8}{x}\)

\(\therefore x+\frac{8}{x}≥4 \sqrt{2} \)

式(1)' を用いて
\( a+\frac{1}{a} ≥ 2\sqrt{a \cdot \frac{1}{a}}=\color{red}{2} \ \)

公式に対し\(a=a, \ b=\frac{1}{a}\)
最小値は \( a=\frac{1}{a}\)のときであるから。

\(a=1\)である。　またこのときは等号が成立する。

または、上式を展開して解くと：

\( a+\frac{1}{a}=2\)
\( a^2+1=2a\)
\( (a-1)^2=0\)
\(\therefore a=1\)

∴最小値は2（\(a=1\)のとき）

---

　　　　

重みつき平均と呼ばれ、各データに重み（重要度、人数…などいろいろあります）を加味した平均です。
加重平均 \(N_g\) は次式で表せる。（\(x_i\):データ　、\(ｇ_i\)：その重み）　

\(N_g= \frac{x_1 g_1+x_2 g_2 + \cdots + x_n g_n}{g_1+g_2 + \cdots + g_n}\)

下表はA社の月給のデータ（年齢20~40代）

はじめから正解を書きます。（加重平均を使い）
A社の平均月給料は：
\(N_g= \frac{25\times60 + 30\times40 + 35\times20}{60+40+20}\) \(=\frac{3400}{120}\) \(=28.3\) （万円） です。

間違えて算術平均を使うと：
\(N_a= \frac{25+30+35}{3}＝30.0\) （万円） です。(間違い)

---

　　　　

・１、２段目の稼働日と株価は集計の生データです。
・３段目のが移動平均、ここでは５日平均としました。

・移動平均は以下のように計算する。
 １日から５日までの算術平均を５日目に記入。
 ２日から６日までの算術平均を６日目に記入。
 \( \qquad \vdots　\qquad　\vdots　 \)
 ３６日から４０日までの算術平均を４０日目に記入。

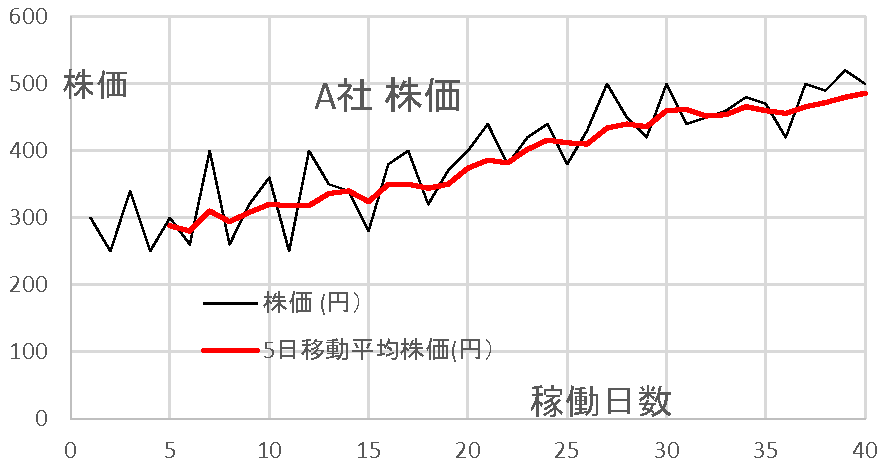
・以上のデータをグラフ化します。

---

　　　　　　　　　　　　　

[コーヒーブレイク/閑話］…お疲れさまでした

移動平均の応用例
株式投資のツールに利用されています。
fig1 はゴールデンクロスと呼ばれ、株式の購入のサインとされている。

fig2 はデッドクロスと呼ばれ、株式の売却のサインとされている。

詳しくは以下の参考リンクを訪問して下さい。

ここはほどほどにして次に進みましょう。

参考リンク先
1. お金のキャンパス
2. 野村証券(1)
3. 野村証券(2)