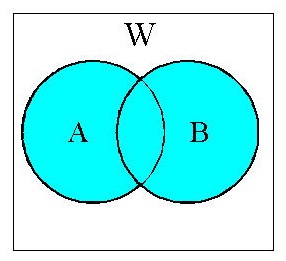
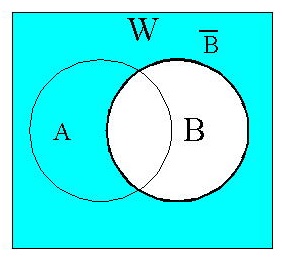
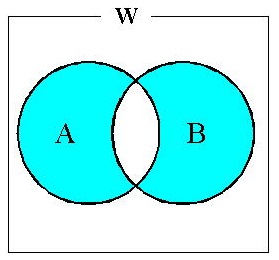
代表的な集合をベン図 (集合の関係を図式化したもの)を用いて表しました。 また図では集合全体を 「W」としています。
(1)和集合:A∪B (A cup(カップ) B)
(union/sum of set)
A∪B = AまたはB = A or B
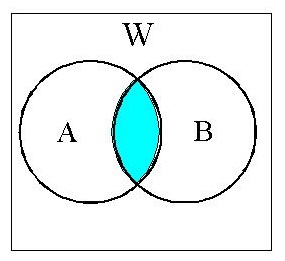
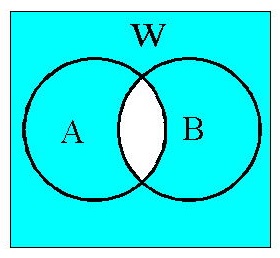
(2)積集合:A ∩ B (Acap(キャップ)B)
(product set)
A∩B= AかつB= A and B
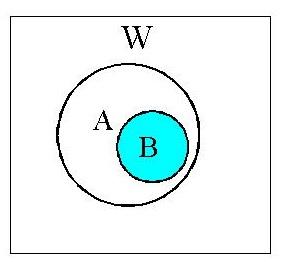
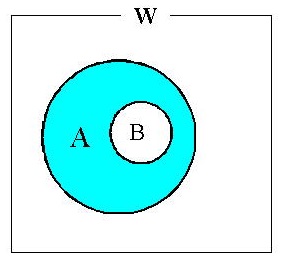
(3)部分集合:B ⊆ A BはAの部分集合
(subset)
これは A∩B=B ともいえる。
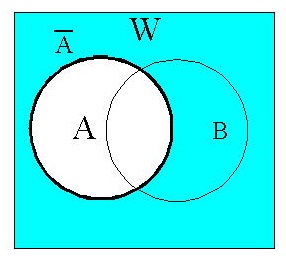
(4)補集合:\( \overline{ A } \) (上バーは notA のこと)
(complement/complementary set)
Aには属さないがWに属する全ての要素の集合。
図(4)の差集合 W∖A (=W-A)でもある。 全体集合Wの明記がなければ補集合\( \overline{ A } \)と表す。
(5)補集合:\( \overline{ B } \)… その他(4)と同様
(6)上記(4)と(5)の和集合 (\( \overline{A} \)) ∪ (\( \overline{B} \))
これは \( \overline{A∩B} \) とも書ける。(後述するドモルガンの法則による)
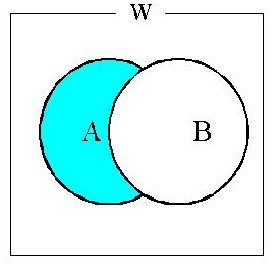
(7)差集合 A∖B (=A-B) ( = A ∩\( \overline{B} \)でもある)
(8)差集合 A∖B (=A-B) ( = A ∩\( \overline{B} \)でもある)
(9)排他的論理和(参考)
(exclusive or)
(A∩\( \overline{B} \))∪(\( \overline{A}\)∩B)=(A∪B)∩(\( \overline{A} \)∪\( \overline{B} \))
=
(A∪B)/(A∩B)…差集合
最後の式を言葉にすると「
AまたはB、ただし AかつB は含まない」となる。
(10)空集合:要素がない集合のこと。
記号は \( \emptyset \) (または Ø ファイ)
例 A={1,2,3} B={4,5,6}のとき
AとBの和集合は空集合… A∪B= \( \emptyset \)
(11)真部分集合:B⊂A
BはAの部分集合かつ A≠B である集合。