湘南理工学舎・実数・数の分類

1、2、3 …
すなわち正の整数です。
注：0 だけ独立して書きましたが、0 を自然数として扱っている本もあります。
　

0、±1、±2、±3 …

整数　\({a}\), \({b}\) を用いて \( \frac{a}{b}\) という分数の形で表せる数。
有限小数、循環する無限小数は有理数です。
また \( \frac{0}{b} \) が成り立つ,ただし\( b≠0 \)。
(何故なら0は整数である。また\(　b=0 \)のとき \( \frac{0}{0} \)の不定形になるから分母\( b≠0 \)が条件)　
例えば 0.2 は…有理数の小数表示。分数表示なら \( \frac{2}{10} \)となる。
有理数の分数は必ず既約分数にでき、既約分数にした a と bは互いに素の関係にある。
有理数には稠密性の性質がある。稠密性については【補足】で説明しています。

有理数ではない実数、つまり分子・分母ともに整数で表すことのできない実数。（実数から有理数を省いた数）
無理数は循環しない無限小数である。無理数には稠密性の性質（有理数より密度が大きい）がある。
例： \(\sqrt{2}\) , \(\sqrt{5}\) , \(\pi\) , \( {e} \)（ネピア数）　

有理数(整数、分数)、無理数を含めた数。
実数は連続性をもって数直線上を稠密にビッシリと埋めつくせる。また四則演算について閉じている。
さらに連続性（完備性）をもつ。

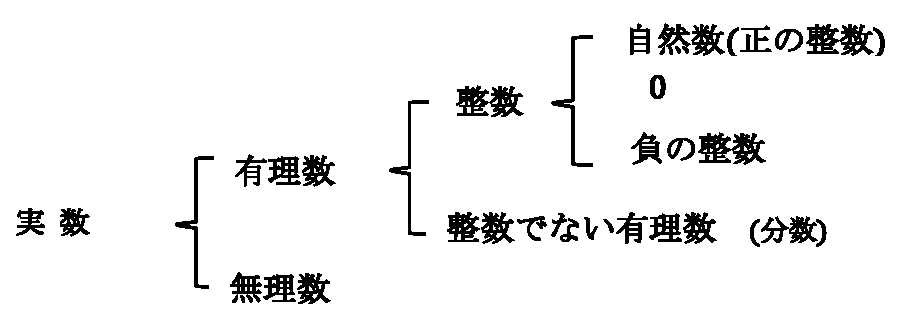
•上の体系図は見慣れた図ですね、特に疑問もなく当たり前のように見てますが、実数が明らかになるまでには長い歴史があったようです。
この種の議論には深いもの(専門分野)があります。また数には複素数もありますが、これについてはどこかで扱うことにして、ここでは省きます。

•整数は、「割り算について閉じて」いないとは…
整数どうしの四足演算のなかで、以下の様に割り算での答えは整数にならないことがある。

　 \(　7+2=9, \quad 9-2=7, \quad 2 \times 8=16\)…加・減・乗の答えは整数になる。

　 \(1 ÷3 =\frac{1}{3}\)…除算の答は整数にならない。

このことを「整数は割り算について閉じていない」と言う。

•有理数は、「四則演算において閉じている。」
有理数の演算は整数どうしの四足演算について、以下の様に答えは必ず有理数になる。

\( 2+ \frac{2}{3}=\frac{8}{3}\), \( 2-\frac{2}{3}=\frac{4}{3} \)

\(4\times \frac{2}{4}=\frac{8}{4}\), \( \frac{6}{5}\)÷\( \frac{1}{2}=\frac{12}{5}\)

四足演算での答えは全て有理数である…このことを「有理数は四則演算についていて閉じている」と言う。

•数直線とは数直線上の点（大きさのない）と数が対応し（点の集まりの直線）…大きさががない点だから直線上を埋め尽せる。
（直線上に数値が乗っているのではない）

•有理数と無理数には稠密性があるという性質……簡単にいうと、数直線のどんな狭い区間を取ってきてもその区間には有理数/無理数が存在するというような意味。

•また、実数には完備性（連続性ともいう）の性質があり、稠密性より密であり、ぎっしり詰まっているというようなイメージ。
完備とは…連続性についてのこと。
数の歴史は「自然数→整数→有理数→無理数→実数」のように拡張/拡大してきました。
（さらなる新しい数がある可能性は？…数学者にお任せします）
実数の「完備性、連続性、コーシー列など」については解析学の分野です。
…ここではこの程度にしておきます。

coffe

[コーヒーブレイク/閑話］…

無理数の発見から公理になるまの期間(時代)…なんと2千年以上かかったのです。

無理数は1872年、英国のデテキントによって「デテキントの切断（Dedekind Cut）」で定義されました。
紀元前の…ピタゴラスの定理より \( a^2 + b^2 = c^2 から　C=\sqrt{a^2+b^2} \) …（直角3角形の斜辺C、他の2辺=a,b）　
　ここで　\( a=1, b=1\) なら… \( C=\sqrt{1^2+1^2} =\sqrt{2}\)　
であるから、簡単に無理数の\(\sqrt{2}\)が得られます。
ピタゴラスの定理は紀元前500年代に発見された定理ですが、この時に無理数の存在が判っていたことになります。　
ピタゴラスの弟子が有理数では説明できない数を発見したとされている…それが\(\sqrt{2}\) です。
無理数の存在認識・予想から証明し、公理になるまでなんと長い・長い時代を要したことになります。
数学の証明の厳格さがでていますね！

数について

•数(実数)の一般的分類

•自然数 ℕ (natural number)

•整数 ℤ (integers)

•有理数 ℚ (rational number)

•無理数 □ (irrational number)

•実数 ℝ (real number)

[コーヒーブレイク/閑話］…