遠隔作用と近接作用
クーロンの法則
距離\(~r~\)を隔てた2つの電荷\(~Q~\)と\(~q~\)には
\[F=k_0 \frac{Qq}{r^2}=9.0\x 10^9 \frac{Qq}{r^2} \tag{1}\]
の力, クーロン力が働く。お互いの距離が10光年離れていても, 瞬時に働く。遠隔作用と呼ぶ。
真空中で1クーロンの2つの電荷が, 距離\(~1m~\)離れているとき, 凡そ90億\(~N~\), 9億\(~Kg~\)重の力が働く。
一体どうしてこんな単位になってしまったのだろう?
力の向きを含めて(1)式を
\[\Vec F=k_0 Qq \frac{\bm{r}}{{r}^3} \tag{2}\]
と書く場合もある。
電荷\(~Q~\)を原点に置き, 電荷\(~q~\)の位置ベクトルを\(~\bm{r}~\)とすれば, \(~\bm{r}~\)方向の単位ベクトルが\(\displaystyle\frac{\bm{r}}{|\bm{r}|}\)となる。
これに対し電荷\(~Q~\)が距離\(~r~\)の地点に
\[\Vec E=\frac{Q}{4\pi\varepsilon_0} \frac{\bm{r}}{\bm{r}^3} \tag{3}\]
の電場を作り, その点に電荷\(~q~\)をおくと
\[\Vec F=q \Vec E=\frac{Qq}{4\pi\varepsilon_0}\frac{\bm{r}}{\bm{r}^3} \]
の力が働くと解釈する。同じクーロン力であるが光の速さで伝わってゆく。近接作用と呼ぶ。
\(\varepsilon_0~\)は
\[k_0=\frac{1}{4\pi\varepsilon_0}=c^2\x 10^{-7} \]
となるように決められた。\(\varepsilon_0~\)を真空の誘電率というが, 光の速さから決められた値である。
ところで(2)式と(3)式は\(~k_0= 1/4\pi\varepsilon_0~\)を使えば全く同じように見えるがそうではない。
(2)式の\(~\Vec F~\)は\(~Q~\) と\(~q~\)を結ぶ直線上に存在するたった一つのベクトルであるが, (3)式の\(~\Vec E~\)は\(~Q~\)の四方八方に存在する
ベクトル場である。
ベクトル場とは, 空間のすべての点において, その点\((x,y,z)\)を始点とするベクトルが定義されているベクトルの集合のことである。
ガウスの法則
なぜ電気力線の密度を電場の大きさとするのか, なぜ\(~\varepsilon_0~\)で割るのか?
電荷\(~+Q~\)から出る電気力線の数\(~N~\)は, 電気力線が実在であっても, あるいは便宜的なものであっても, \(~N\propto Q^2~\)とかではなく, \(~N\propto Q~\)として良いだろう。(\(+Q~\)から\(~N~\)本出ていれば, \(+Q~\)を2つ集めた\(+2Q~\)からは\(~2N~\)本出ているだろう)
点電荷\(~Q~\)を中心とする, 半径\(~r~\)の球面を通過する単位面積当たりの電気力線の本数, すなわち電気力線の密度は,
\[n=\frac{N}{4\pi r^2}\]
である。一方その球面の位置における電場の大きさは
\[E=\frac{1}{4\pi \varepsilon_0}\frac{Q}{r^2} \]
である。2式を比べて
\[E=\frac{Q}{\varepsilon_0 N}n \]
となり, 電場の大きさは電気力線の密度に比例する。
せっかくなのでついでに
\(~N=Q/\varepsilon_0~\)とすれば\(~E=n~\)となる。この
\[~N=\frac{Q}{\varepsilon_0} \tag{4} \]
をガウスの法則と呼ぶ。言葉で表現すれば,
「真空中で\(+Q~\)[C]の電荷を取り囲む, 任意の閉曲面から出ている電気力線の総数は\(\displaystyle~\frac{Q}{\varepsilon_0~}\)である」となる。
\(\varepsilon_0~\)で割った理由は
ついでに割っただけである。「ついで」では少々不親切だ。
単位の制定には長い歴史がある。そもそも, 電荷も磁荷もその実態が分からない中で電磁気学は発展してきた。
新たな物理量を定義するにはそれまでに確立していた長さ・質量・時間の概念に基づいて定義するしかない。絶対単位系という。
前に真空の誘電率\(~\varepsilon_0~\)は光の速さから決められたと書いたが, 真空なので誘電作用はあるはずもない。
\(~\varepsilon_0~\)は古典的な力[\(N\)](ニュートン)と新しく発見された物理量
[\(C\)](クーロン)との辻褄を合わせるために導入された量である。
電磁気学の発展に大きく貢献したヘビサイドは, \(~4\pi~\)をも含めた\(~MKSA~\)有理化単位系のメリットを強調した。
ガウスの法則は,
(1) 電場の大きさ\(~E~\)が, 電気力線の密度と等しくなるように, クーロンの法則を言い換えた。
(2) クーロンの法則のベクトル\(~\Vec F~\)は一本のみであるが, ガウスの法則のベクトル\(~\Vec E~\)は無数にある。
と言える。(かなり主観が強いので要注意)
ガウスの法則の適用
分布する電荷が作る電場 先ずはクーロンの法則で解いてみよう。
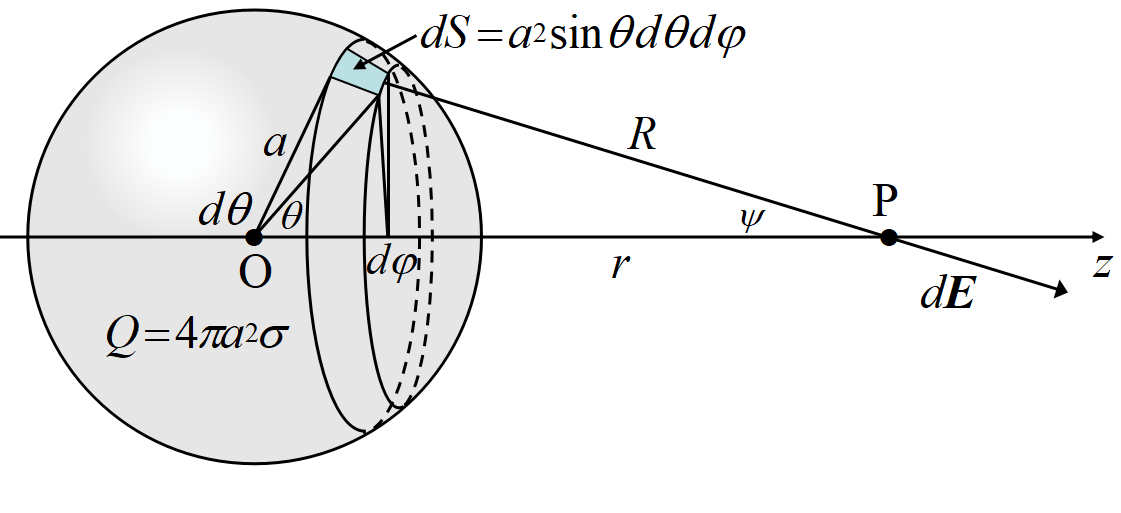
面密度\(~\sigma\)で帯電した, 半径\(~a~\)の導体球の作る電界の大きさを求める。
点 O を中心として\(~z~\)軸から角\(~\theta~\)の位置の微小球面\(~dS=a^2 sin\theta d\theta d\phi~\)にある電荷は, \(~dQ= \sigma dS~\)である。
これが点\(~P~\)に作る電場の\(~z~\)成分は, 総電荷量\(~Q= 4\pi a^2\sigma\)を用いて,
\[dE= \frac{1}{4\pi \varepsilon_0}\frac{dQ}{R^2}cos \psi
= \frac{Q}{(4\pi)^2 \varepsilon_0} \frac{sin \theta d\theta d\phi}
{R^2}cos\psi\]
となる。これを先ず\(~z~\)軸のまわり, 即ち\(~\phi~\)について積分する。
\[\begin{align}
dE&= \frac{Q}{(4\pi)^2 \varepsilon_0}\int_{0}^{2\pi}\frac{sin \theta d\theta d\phi}{R^2}cos\psi \\
&= \frac{Q}{8\pi \varepsilon_0}\frac{sin \theta d\theta}{R^2}cos\psi
\end{align}\]
となる。一方電場の\(~z~\)軸に垂直な成分は対称性により積分は\(~0~\)となる。よって求める電場は\(~z~\)軸方向を向き, 大きさは上式を\(~\theta~\)で積分すれば良い。
\[
E= \frac{Q}{8 \pi \varepsilon_0}\int_{0}^{\pi}\frac{sin \theta cos\psi d\theta}{R^2}
\]
ここで余弦定理\(~R^2= a^2 + r^2 -2arcos\theta~\)を\(~\theta~\)で微分すると, \(~a,r~\)を定数として,
\[Rdr=arsin\theta d\theta\]
であり, また\(~a^2= R^2 +r^2 -2Rrcos\psi~\)より, \(~cos\psi~\)を\(~R~\)で置き換えて,
(1) 点\(~P~\)が球の外側の時
\[\begin{align}
E&= \frac{1}{4\pi\varepsilon_0}\frac{1}{4a}\int_{r-a}^{r+a} \left(1+\frac{r^2 -
a^2}{R^2}\right)dR \\
&= \frac{1}{4\pi\varepsilon_0}\frac{1}{4a} \left[R-\frac{r^2 - a^2 }{R}
\right]^{r+a}_{r-a} \\
&= \frac{Q}{4\pi\varepsilon_0 r^2} \tag{5}\\
\end{align} \]
(2) 点\(~P~\)が球の内側の時
\[\begin{align}
E&= \frac{1}{4\pi\varepsilon_0}\frac{1}{4a}\int_{a-r}^{r+a} \left(1+\frac{r^2 -
a^2}{R^2}\right)dR \\
&= \frac{1}{4\pi\varepsilon_0}\frac{1}{4a} \left[R-\frac{r^2 - a^2 }{R}
\right]^{a-r}_{r-a} \\
&= \frac{Q}{4\pi\varepsilon_0 r^2} \tag{6}\\
\end{align}\]
となる。すなわち球の内部での電場は\(~0~\), 外部は中心に点電荷\(~Q~\)を置いた時と等しい。
ガウスの法則を用いると上記の積分操作は不要で, 電気力線\(~N= Q/\varepsilon_0 ~\)を円の表面積\(~4\pi r^2 ~\)で割って, (5)式が直接求まる。
コンデンサー内部の電場(1)
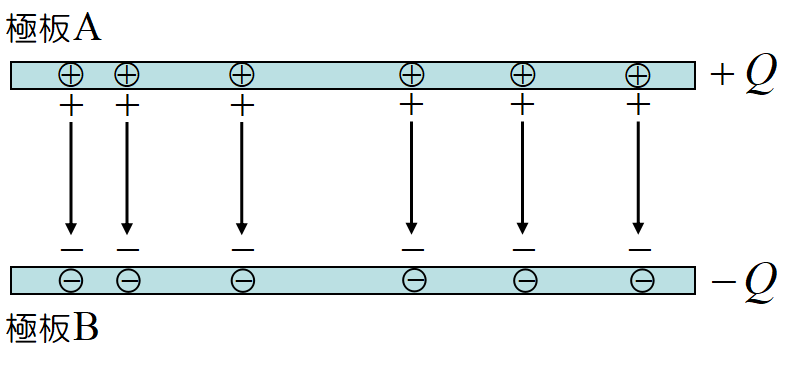
\(+Q~\)と\(-Q~\)に帯電した, 極板の面積\(~S~\)の平行板コンデンサーの電場を求めてみよう。
電気力線は正電荷から出て負電荷に入ると習ったせいか, 電気力線の総数は\(~N=Q~\)と勘違いすることがままあるので注意。
(4)式より, 電荷\(~Q~\)から出る電気力線は\(~N=Q/\varepsilon_0\)。\(~Q=1~\)すなわち
+1の電荷から-1の電荷に至る電気力線は1本ではなく, \(\displaystyle \frac{1}{\varepsilon_0}\)本である。
従ってコンデンサー内の電気力線の総数は
\[N=Q\x \frac{1}{\varepsilon_0}=\frac{Q}{\varepsilon_0}\]
本となる。単位面積当たりの本数が電場の大きさであるから, 極板の面積\(~S~\)で割って
\[E=\frac{Q}{\varepsilon_0 S} \tag{7}\]
と, お馴染みの式となる。
コンデンサー内部の電場(2) こちらが正統的なガウスの法則による解法
面積\(~S~\), 間隔\(~d~\)の極板に\(~+Q~\),\(~-Q~\), の電荷が分布しているとする。
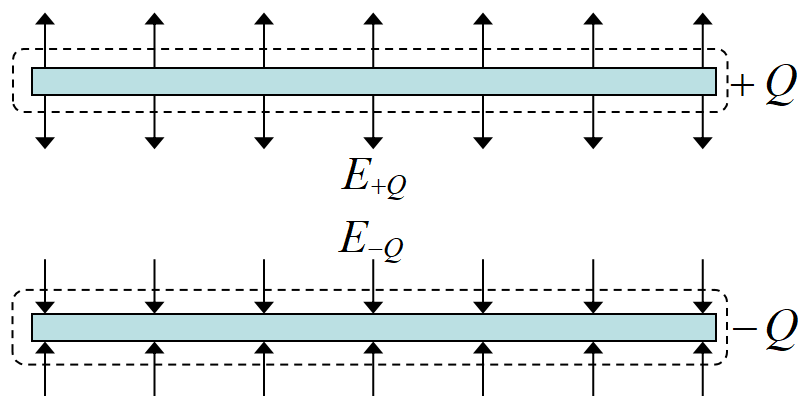
電気力線は極板の上下に出ているから, ガウスの法則を適用する場合, 面積は\(~S~\)ではなく\(~2S~\)である。
\[E_{+Q}\x 2S= \frac{Q}{\varepsilon_0} \]
すなわち
\[E_{+Q}= \frac{Q}{2 \varepsilon_0 S} \]
電荷\(~-Q~\)も同様の電場を生成するから, 中央部の電場は,
\[E=E_{+Q}+E_{-Q}= \frac{Q}{\varepsilon_0 S} \]
と, (7)式と同じ結果を得る。電極外部(図の上下)では, 電場\(~E_{+Q}, E_{-Q}~\)が打ち消しあい0(ゼロ)となる。
直線上の電場はなぜ一様にならない?
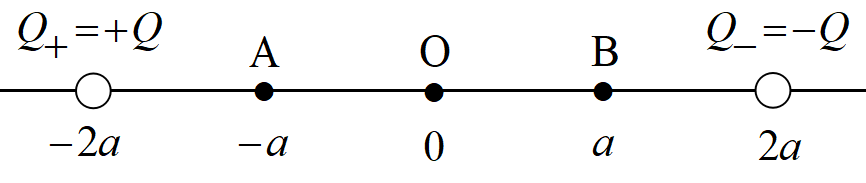
直線上\(-2a~\)と\(+2a\)の位置に\(+Q~\)と\(-Q~\)の電荷があるとする。
この時コンデンサーを思い浮かべ, 直線上は一様な電界では?との質問を時々受ける。
実際に計算してみよう。
この時, \(~A, O, B~\)の電場の大きさは
\[\begin{align}
E_A &=\frac{k_0 Q_{+}}{a^2}+\frac{k_0 Q_{-}}{9a^2}=\frac{10 k_0 Q}{9a^2}\\
E_O &=\frac{k_0 Q_{+}}{4a^2}+\frac{k_0 Q_{-}}{4a^2}=\frac{k_0 Q}{2a^2} \\
E_B &=\frac{k_0 Q_{+}}{9a^2}+\frac{k_0 Q_{-}}{a^2}=\frac{10 k_0 Q}{9a^2}\\
\end{align}\]
となり, 位置\(~O~\)が最小となる。
コンデンサー内では電気力線は放射状に拡がらないから, 逆2乗法則は使えない。ガウスの法則を使って, 一定値\(E= Q/\varepsilon_0 S\)となる。
直線上の電荷は電気力線は放射状に拡がるので, 普通にクーロンの法則を適用する。