微分積分・定積分|湘南理工学舎・

関数\(f(x)\) は閉区間[a,b] で有界（f(x)に上限、下限がある）な関数とする。
閉区間[a,b]について次の小区間を考える：
\(Δ :\ (a=)x_0<x_1<x_2<…x_i<\) \(…x_{n-1}<x_n(=b)\)

の関係において、 \(Δ_i=x_i-x_{i-1}\) のような区間に分ける。

・\(Δ\)を閉区間[a,b]の\(Δ\)分割という。（分割\(Δ\)ともいう）

・\(C_i\) は小区間 \(Δ_i\) の代表点 という。
\(C_i\) は小区間内で任意です。（中心でなくてよい）

・\(x_i\) を分点という。

・\(|Δ|\) は小区間 \(Δ_i\)　の中で最大のもの。
（下の定義のなかで使います）

ここで\(f(x)\) とx軸と区間a とb で囲まれた面積 \(S_r(\Delta)\) を考えます。

小区分 \(Δ_i=x_i-x_{i-1}\)の面積は:
\(ΔS_i=f(c_i)Δ_i\) です。

\(S_i\)の総和は\(S_r(\Delta)\)：
\(S_r(\Delta)\)\(=\displaystyle \sum_{i=1}^n ΔS_i\)\(=\displaystyle \sum_{i=1}^n f(c_i)Δ_i\) \(=\displaystyle \sum_{i=1}^n f(c_i) (x_i-x_{i-1})\)

これを リーマン和 といいます。

このリーマン和により定積分を次のように定義します。

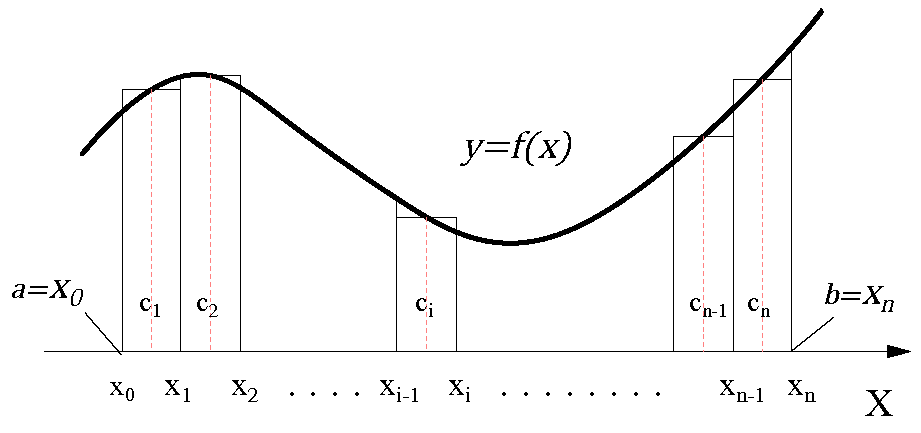
【定積分の定義2】（リーマン和による）

関数\(f(x)\) が閉区間 [a, b ] において有界とする。
\(S_r(\Delta)\)\(=\displaystyle \sum_{i=1}^n f(c_i)Δ_i\) \(=\displaystyle \sum_{i=1}^n f(c_i) (x_i-x_{i-1})\)　\(\ :(a)\)

は分割の\(n\) を大きく、 \(|Δ| \rightarrow 0\) の極限において、代表点\(c_i\) のとり方によらず
\( S=\displaystyle \lim_{ |Δ| \to 0 } \displaystyle \sum_{i=1}^n f(c_i) (x_i-x_{i-1})\) \(\ :(b)\) 【※】

が成立、すなわち上式がある値\(S\) に収束するとき積分可能となる。
これをリーマン積分可能、リーマン可積分、単に可積分などという。

そして
\(\int_a^b f(x) dx=\displaystyle \lim_{ |Δ| \to 0 } \displaystyle \sum_{i=1}^n f(c_i) (x_i-x_{i-1})\) \(\ :(c)\) 【※】
【※】:\(|Δ| → 0 \)とは\(\sum\) にかかる\(n\)は「\(n → \infty \)」となる。　　

をリーマン積分といい、これを閉区間\([a,b]\) の定積分として定義している。
この定積分は\(f(x)\) とx軸と区間a とb で囲まれた面積 \(S\) を示す。

f(x) は連続だから、Δ分割の代表点をどの位置にとっても、分割の中での\(f(c_i)\) は下限と上限の間にあり発散せず、ある値に収まることに留意。
また \(|Δ| \rightarrow 0\)　なので式(b),式(c)は収束する。

一般的に積分可能な条件は「\(f(x)\)が有界で連続な関数」です。
さらに強い条件は「\(f(x)\)が有界で一様連続な関数」です。
しかし閉区間\([a,b]\)に不連続があり有界でない場合でもこれから学ぶ定積分を拡張した「広義積分」により定積分が可能になることがあります。

3.定積分の性質

• \(\int_a^b k f(x) dx = k \int f(x) dx \) (k:定数)

• \( \int_a^b \left( f(x) + g(x) \right) dx\) \( =\int_a^b f(x) dx + \int_a^b g(x) dx \)

• \( \int_a^b f(x) dx\) \( =\int_a^c f(x) dx + \int_c^b g(x) dx \)

• \(\int_a^a f(x) dx =0\)

• \(\int_a^b f(x) dx = - \int_b^a f(x) dx \)

• \( \left| \int_a^b f(x) dx \right| \)\( ≤ \int_a^b |f(x)| dx \)

• \(\int_a^b f(x) dx = (b-a) f(c) \) \((a<c<b)\) (※1)
（積分平均値の定理）

• \( \left(\int_a^b f(x)g(x) dx \right)^2\)\( ≤ \int_a^b f(x)^2 dx \cdot \int_a^b g(x)^2 dx \)　(※2)
（シュワルツの不等式）（ドット「・」は内積記号です）

上式の（※1）と（※2）の証明

（※1）の証明
平均値の定理より【参照先】
関数\(f(x)\) が閉区間\([a,b]\)で連続であれば、
\( \frac{\int_a^b f(x) dx}{(b-a)}\)\(=\frac{F(b)-F(a)}{(b-a)}\)\(=F'(c)=f(c)\)

となる\(c\) が定義域の閉区間\([a,b]\)に存在する。

（※2）の証明
【参照先】
証明の方針は：
\( f(x)=ax^2+bx+c≥0\) の式を作り：
\(\frac{D}{4}=b^2-ac ≤0 \) より \(b^2≤ac\) であることを利用する。
ここでは以下のようにx　の代わりにt に関する2次方程式の判別式\(D\) が 0 以下であることが不等式が成立する条件です。
また\(a, b, c\)のかわりに \(c, d, e\) を使っています。
また定積分の結果は定数の\(c, d, e\)　です。

次の式を考えて、これを変形して t についての2次方程式を作る。
\(\underline{ \int_a^b　\left( tf(x)-g(x) \right)^2 dx ≥0 }\) （変数t は実数）
左辺は2乗だから、上の不等式が成立する。
上の不等式を展開していくと目的の証明を得る。

\( \int_a^b\left( t^2 f(x)^2-2tf(x)g(x)+g(x)^2\right)dx≥0 \)

\( t^2\int_a^b f(x)^2dx- 2t\int_a^bf(x)g(x)dx\)\(+\int_a^b g(x)^2 dx ≥0 \)

ここで、 \(\int_a^b f(x)^2dx=c\) \(,\ \int_a^bf(x)g(x)dx=d\) \(,\ \int_a^b g(x)^2 dx=e\) とする。

（定積分の結果は定数です）

上式は次のt の2次方程式（不等式）に変形できる。
\(\underline{ ct^2-2dt+e ≥0 }\)
この不等式の判別式により証明をする。

2次不等式が成立する条件は次の2次方程式が\(y=0\) 以上にあること。
（解である\(t\) は \(y\)軸と交わらない。（接することはある））

\(y=ct^2-2dt+e \)

【参照先】
そのために、判別式\(D≤0\) であること。
すなわち：
\(\frac{D}{4}=\frac{(2d)^2-4ce}{4}\)\(=d^2-ce≤0\)

\( \therefore d^2≤c\ e\)

\( \therefore \left(\int_a^b f(x)g(x) dx\right)^2\)\( ≤\int_a^b f(x)^2dx \cdot \int_a^b g(x)^2 dx \)

例題

[1] \(\int_0^1 \sqrt{x} dx\)

\(\int_0^1 \sqrt{x} dx\)\(=\int_0^1 x^{\frac{1}{2}} dx\)\(= [\frac{2}{3} x^{\frac{3}{2}}]_0^1 \)

\(= \frac{2}{3}[1-0]\) \(=\frac{2}{3}\)

[2] \(\int_0^{\frac{\pi}{2}} sin{x} dx\)

\(\int_0^{\frac{\pi}{2}} sin{x} dx\)\(=[-cos\ x]_0^{\frac{\pi}{2}} \)

\(=[-0+1]=1\)

[3] \( \int_0^1 (3x + 2)^3 dx \) （置換積分の例）

\( 3x + 2＝t \) と置換し、\( \frac{dt}{dx}=3 \)　\( dx= \frac{1}{3}t\)
積分範囲も置換する。
\(\color{red}{ x=0 \rightarrow t=2 \quad x=1 \rightarrow t=5}\)
\( \int_0^1 (3x + 2)^3 dx = \int_2^5 t^3\ dx \) \(= \int_2^5 t^3\ \frac{1}{3}\ dt\) \(= \frac{1}{3} \int_2^5 t^3\ dt \)
\(= \frac{1}{12}[t^4]_2^5\ \) \(=\frac{203}{4}\)

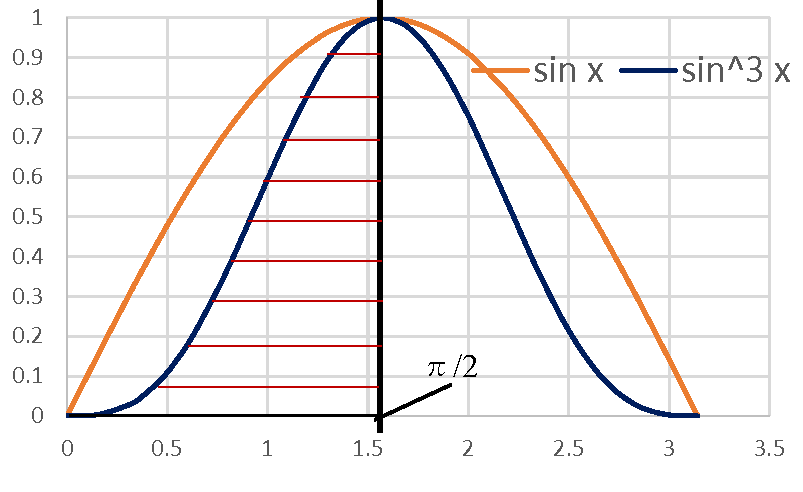
[4] \(I_n= \int_0^{\frac{\pi}{2}} sin^n x dx\)
（部分積分の例）

次のように\(sin^nx\)　を積の積分に分解してから展開する。

\(I_n=\int_0^{\frac{\pi}{2}} sin^n x dx\) \(=\int_0^{\frac{\pi}{2}} (sinx) (sin^{n-1}x)dx\) \(=\int_0^{\frac{\pi}{2}} (-cosx)' (sin^{n-1}x)dx\)

\(=[(-cosx)(sin^{n-1}x)]_0^{\frac{\pi}{2}}\)\(-\int_0^{\frac{\pi}{2}} (-cosx)(n-1)(sin^{n-2}x)cosx dx\)
(\( (sin^{n-1}x)'=(n-1)(-cosx)(sin^{n-2}x) \) )

\(=0　- \int_0^{\frac{\pi}{2}} (n-1)(sin^{n-2}x)cos^2 x dx\)

\(= \int_0^{\frac{\pi}{2}} (n-1)(sin^{n-2}x)cos^2 x dx\)

\(= \int_0^{\frac{\pi}{2}} (n-1)(sin^{n-2}x)(1-sin^2 x) dx\)

\(=(n-1) ( \int_0^{\frac{\pi}{2}} (sin^{n-2}x)dx\)\(-\int_0^{\frac{\pi}{2}} sin^n x) dx ) \)

\(=(n-1)I_{n-2}-(n-1)I_n \)\(=(n-1)I_{n-2}-nI_n + I_n \)

\( \therefore I_n=\frac{(n-1)}{n}I_{n-2}\)　

の漸化式がえられました。
漸化式\(I_n\) が2 飛びが特徴です。

[5]上記の結果より \(I_6\)と\(I_7\)を求めよ　

予め\(I_0\)と\(I_1\)を求めておく
\(I_0= \int_0^{\frac{\pi}{2}} sin^0 x dx\) \(I_0= \int_0^{\frac{\pi}{2}} 1dx\) \(=[x]_0^{\frac{\pi}{2}}\)\(=\frac{\pi}{2}\)

\(I_1= \int_0^{\frac{\pi}{2}} sin x dx\)\(=[-cos x]_0^{\frac{\pi}{2}}=1\)

\(I_6= \int_0^{\frac{\pi}{2}} sin^6 x dx\)\(=\frac{6-1}{6}I_{(6-2)}\)\(=\frac{5}{6}I_{4}\) \(=\frac{5}{6} \frac{(4-1)}{4}I_{(4-2)}\)\(=\frac{5}{6} \frac{3}{4}I_{2}\) \(=\frac{5}{6}\frac{3}{4}\frac{1}{2}I_{0}\) \(=\frac{5}{6}\frac{3}{4}\frac{1}{2}\frac{\pi}{2}\)
\(=\frac{15}{96} \pi=\frac{6}{32} \pi\) （\(n\) が偶数でした）

\(I_7= \int_0^{\frac{\pi}{2}} sin^7 x dx\)\(=\frac{6}{7}I_{5}\)\(=\frac{6}{7}\frac{4}{5}I_{3}\) \(=\frac{6}{7}\frac{4}{5}\frac{2}{3}I_{1}\) \(=\frac{6}{7}\frac{4}{5}\frac{2}{3} \cdot 1\)
\(=\frac{48}{105}\)\(=\frac{16}{36}\) （\(n\) が奇数でした）

例題[4][5]から次のウォリスの公式を導きだせます。

ウォリスの公式

\(I_n= \int_0^{\frac{\pi}{2}} sin^n x dx\) ：❶ とする。
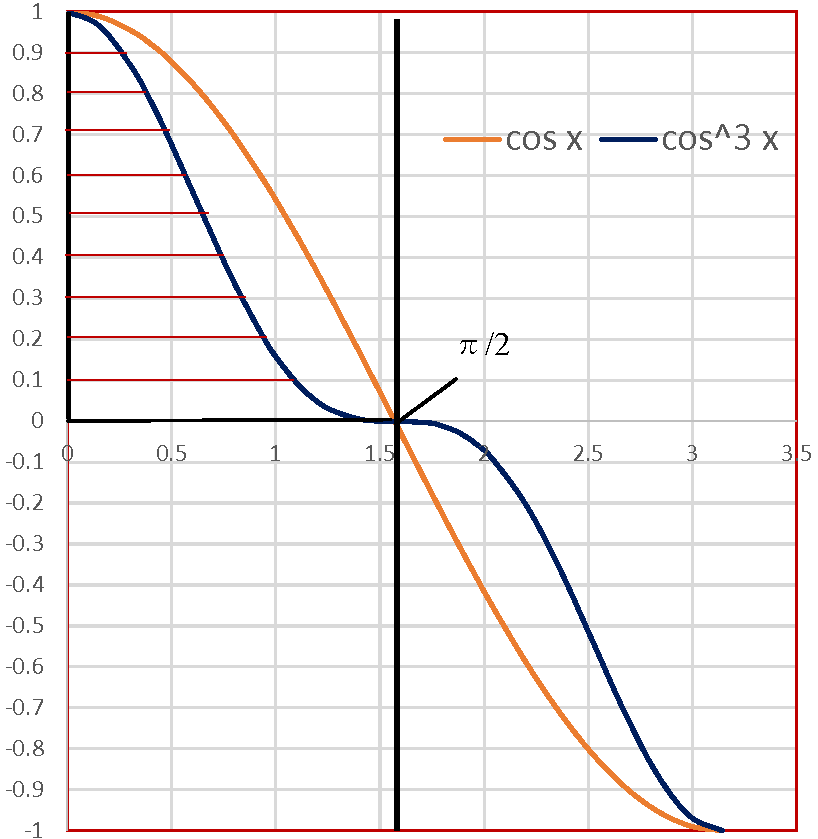
また\(n\)は非負、2以上とする。
　 \(I_n=\frac{(n-1)}{n}I_{n-2}\)　：❷

また次式が成り立つ
\(\displaystyle \lim_{ n \to \infty } \frac{2}{1}\frac{2}{3}\frac{4}{3}\frac{4}{5}\frac{6}{5}\frac{6}{7}\frac{8}{7}\) \( \cdots\underline{\frac{2n}{(2n-1)}\frac{2n}{(2n+1)}}\)\(=\frac{\pi}{2} \) ：❸

下線部が一般項です。
分母と分子の規則性があります、それが一般項です。

これを総乗数の記号を使い表わすと：
\(　\displaystyle \prod_{i=0}^\infty \underline{ \frac{2n}{(2n-1)}\frac{2n}{(2n+1)}}\)\(=\frac{\pi}{2}\) ：❸’
（❸’を展開すると❸になります。疑問の方は試して下さい。）

また：
\(I_n=\int_0^{\frac{\pi}{2}} cos^n x dx\)\(=\int_0^{\frac{\pi}{2}} sin^n x dx\) ：❶'

❸、❸’と❶’ は次に証明します。

❸、❸’ を証明：
式❸の表現を変える。（下式の[]を[A]に変える）
\(\displaystyle \lim_{ n \to \infty } [\frac{2}{1}\frac{2}{3}\cdots\frac{2n}{(2n-1)}\frac{2n}{(2n+1)}]\)\(=\frac{\pi}{2} \)

\(\underline{　\displaystyle \lim_{ n \to \infty } [A]=\frac{\pi}{2}} \)：❸

漸化式❷ を偶数と奇数に分けるとそれぞれ次となる。

\( I_{2n}=\frac{2n-1}{2n}\frac{2n-3}{2n-2}\cdots \frac{5}{6} \frac{3}{4} \frac{1}{2} I_0 \)❺

\(I_{2n+1}=\frac{2n}{2n+1}\frac{2n-2}{2n-1}\cdots \frac{6}{7} \frac{4}{5} \frac{1}{3}I_1\) ❻
（\(I_0=\frac{1}{2}\pi ,\quad I_1=1\) ）

\(\frac{I_{2n+1}}{I_{2n}}=\underline{ \frac{2n}{2n+1} \frac{2n}{2n-1} }\) \(\underline{ \cdots \frac{4}{5} \frac{4}{3} \frac{2}{3} \frac{2}{1}} (\frac{2}{\pi})\) \(=[A](\frac{2}{\pi})\)

\(\frac{\pi}{2} \frac{I_{2n+1}}{I_{2n}}=[A]\)

これより式❸は：
\(\displaystyle \lim_{ n \to \infty } [A]=　\frac{\pi}{2} \displaystyle \lim_{ n \to \infty }\frac{I_{2n+1}}{I_{2n}}\)

すなわち：
\(\displaystyle \lim_{ n \to \infty } \underline{ \frac{I_{2n+1}}{I_{2n}} }=1 \) ❹

が証明できればよい。
式❹の下線部（漸化式の比）が\(n \rightarrow \infty\) のとき「1」に収束すれば❸、❸’が証明できたことになる。

\(0 <x <\frac{\pi}{2}\) に対し

\(0<sinx <1\)

\(0<sin^{2n+1}x < sin^{2n}x < sin^{2n-1}x \)

上式は次に書ける。
\(0<I_{2n+1}< I_{2n} < I_{2n-1}\)

はさみうちを使うので上式を　\(I_{2n+1}\) で割る。
\(\frac{I_{2n+1}}{I_{2n+1}} < \frac{I_{2n}}{I_{2n+1}} < \frac{I_{2n-1}}{I_{2n+1}}\)

\(\frac{I_{2n-1}}{I_{2n+1}}=I_{2n-1} \frac{2n}{2n+1} I_{2n-1}=\frac{2n+1}{2n}\)

\(\displaystyle \lim_{ n \to \infty } \frac{2n+1}{2n} =1\)

\(1< \frac{I_{2n}}{I_{2n+1}} < \frac{2n+1}{2n} \)

\(\displaystyle \lim_{ n \to \infty } \frac{I_{2n}}{I_{2n+1}} =1\) \(=\displaystyle \lim_{ n \to \infty } \frac{1}{　\frac{I_{2n+1}}{I_{2n}} }\)

\(\therefore \underline { \displaystyle \lim_{ n \to \infty } \frac{I_{2n+1}}{I_{2n}} =1 }\)　❹
証明終わり

式❺、❻を２重階乗表示すると：　

階乗記号が2つ ➡「！！」
❺(nは偶数として)：
\(I_n=\frac{(n-1)!!}{n!!} \frac{\pi}{2}\)

❻(nは奇数として)：
\(I_n=\frac{(n-1)!!}{n!!}\)

\(n!!\) は２重階乗といい、2飛びの階乗です。
\(7!!=7\ 5\ 3\ 1=105\)

\(8!!=8\ 6\ 4\ 2=384\)

❶’ の証明:

\(I_n=\int_0^{\frac{\pi}{2}} cos^n x dx\)

\(x=\frac{\pi}{2}-t\) とおき、\(dx=-1dt\)
\(x=0 \rightarrow t=\frac{\pi}{2},\ x=\frac{\pi}{2} \rightarrow t=0\)
\(=\int_{\frac{\pi}{2}}^0 cos^n(\frac{\pi}{2}-t)-dt\)

\(=\int_0^{\frac{\pi}{2}} sin^n t dt\)

記号\(t\)を\(x\)に変えて
\(=\int_0^{\frac{\pi}{2}} sin^n x dx\)

\(\therefore I_n=\int_0^{\frac{\pi}{2}} cos^n x dx\)\(=\int_0^{\frac{\pi}{2}} sin^n x dx\) ：❶'

上式は積分範囲 \([0,\frac{\pi}{2}]\) の領域での\(sinx\) と \(cosx\)　の面積が等しいことを意味しているが、下図のとおり図形は違います。

累乗の\(n\) が増えると鋭い形状になり、面積は小さくなる。

\(x=0 \rightarrow \frac{\pi}{2}\) に対し
・\(sin^3x\)は \(0 \rightarrow 1\) へ増加。
・\(cos^3x\)は \(1 \rightarrow 0\) へ減少。

[コーヒーブレイク/閑話］…