\(M_{ijk}\) :小分割\(V_{ijk}\) における上限値。
\(m_{ijk}\) :小分割\(V_{ijk}\) における下限値。
\(M_{ijk}=sup \{f(x,y,z)|(x,y,z)\in V_{ijk} \} \)
\(m_{ijk}=inf \{f(x,y,z)|(x,y,z)\in V_{ijk} \} \)
\( \begin{cases} U(f,\Delta)= \displaystyle\sum_{i=1}^{ℓ} \displaystyle\sum_{j=1}^m\displaystyle\sum_{k=1}^n M_{ijk} |V_{ijk}| \\ L(f,\Delta)= \displaystyle \sum_{i=1}^{ℓ} \displaystyle\sum_{j=1}^m\displaystyle\sum_{k=1}^n m_{ijk} |V_{ijk}| \end{cases} \)
\(\Delta\)分割を細かくしていくと:
\(\overline{\dsiii}_V f(x,y,z) dxdydz\) \(=inf \{U(f,\Delta) | \Delta:V の分割\}\)
\(\underline{\dsiii}_V f(x,y,z) dxdy\) \(=sup \{L(f,\Delta) | \Delta:V の分割\}\)
\(\dsiii_v f(x,y,z) dxdydz\) \(=\overline{\dsiii}_V f(x,y,z) dxdydz\) \(=\underline{\dsiii}_V f(x,y,z) dxdy\)
(\(K \setminus V\): \(\ K \)と\(D\)の差集合 )
☞※1:(x,y,z) が領域V にあるとき
☞※2:(x,y,z) が領域V 以外の\(K\)平面にあるとき
この関数の出力は「1」「0」に注目し、仮に\(\chi_{V}=1\)なら
\( \chi_{V} \times 面積 V =面積 V \)
高さ1 とは、V は体積でもあるが面積でもある。
\(|V|=\dsiii_V \chi_{V} dx dy dz=\dsiii_V 1 dx dy dz\)
V が体積確定(体積をもつ)とはこの積分ができることである。
V の体積を\(|V|\)で表す。
\( \dsiii_V f(x,y,z)dxdydz\)
\(=\dsii_D dxdy \dsi_{φ_1}^{φ_2} f(x,y,z)dz \)
\(=\dsii_D \left( \dsi_{φ_1}^{φ_2} f(x,y,z)dz \right)dxdy\) \(\ :❶\)
\( \dsiii_V f(x,y,z)dxdydz\)
\(=\dsi_a^b \dsi_c^d \left( \dsi_{φ_1}^{φ_2} f(x,y,z)dz \right)dxdy\)
\(=\dsi_a^b \left( \dsi_c^d \left( \dsi_{φ_1}^{φ_2} f(x,y,z)dz \right) dy \right) dx\) \(\ :❷\)
\( \dsiii_V f(x,y,z)dxdydz\)\(=\dsi_a^b dx \dsi_{\psi_1}^{\psi_2} dy \dsi_{φ_1}^{φ_2} f(x,y,z)dz\)
\(=\dsi_a^b \left( \dsi_{\psi_1}^{\psi_2} \left ( \dsi_{φ_1}^{φ_2} f(x,y,z)dz \right) dy \right) dx \) \(\ :❸\)
\( \dsiii_V f(x,y,z)dxdydz\) \(= \dsi_a^b dx \dsi_c^d dy \dsi_a^b f(x,y,z) dz \)
\(=\dsi_a^b \left( \dsi_c^d \left( \dsi_e^f f(x,y,z)dz \right) dy \right) dx\) \(\ :❹_1\)
\( \dsiii_V f(x,y,z)dxdydz\) \(= \dsi_e^f dz \dsi_c^d dy \dsi_a^b f(x,y,z) dx \)
\(=\dsi_e^f \left( \dsi_c^d \left( \dsi_a^b f(x,y,z)dx \right) dy \right) dz\) \(\ :❹_2\)
\( \dsiii_V f(x,y,z)dxdydz\)\(=\dsi_e^f dz \dsi_a^b dx \dsi_c^d f(x,y,z) dy \) \(=\dsi_e^f \left( \dsi_a^b \left( \dsi_c^d f(x,y,z)dy \right) dx \right) dz\) \(\ :❹_3\)
\( \dsiii_V f(x,y,z)dxdydz\)\(=\left(\dsi_a^b g(x) dx \right) \left(\dsi_c^d h(y) dy \right) \left(\dsi_e^f p(z) dz \right) \) \(\ :❺\)
\( \dsiii_V f(x,y,z)dxdydz\)\(=\dsi_a^b \left( \dsii_E f(x,y,z)dy dz \right)dx\) \( =\dsi_a^b dx \dsii_E f(x,y,z)dy dz \)
変数\(z\) がキーポイント(∵3変数 の関係式だから)
\(z \le 2-x-y \)
\(z=0→y \le 2-x \)
\(y=0→x \le 2 \)
\( \dsiii_V f(x,y,z)dxdydz\) \(=\dsi_0^2 \dsi_0^{2-x} \dsi_0^{2-x-y} 1\ dx dy dz \)
\(= \dsi_0^2 \left( \dsi_0^{2-x} \left( \dsi_0^{2-x-y} 1\ dz \right) dy \right) dx \)
\(=\dsi_0^2 \left( \dsi_0^{2-x} (2-x-y)dy \right) dx\)
\(=\dsi_0^2 [2y-xy-\frac{1}{2}y^2 ]_0^{2-x} dx \)
\(=\dsi_0^2 [2(2-x)-x(2-x)\) \(\ -\frac{1}{2}(2-x)^2 ]_0^{2-x} dx \)
\(=\dsi_0^2 (2-2x+\frac{1}{2}x^2) dx \)
\(=\left[2x-x^2+\frac{x^3}{6}\right]_0^2\)\( =\frac{3}{4}\)
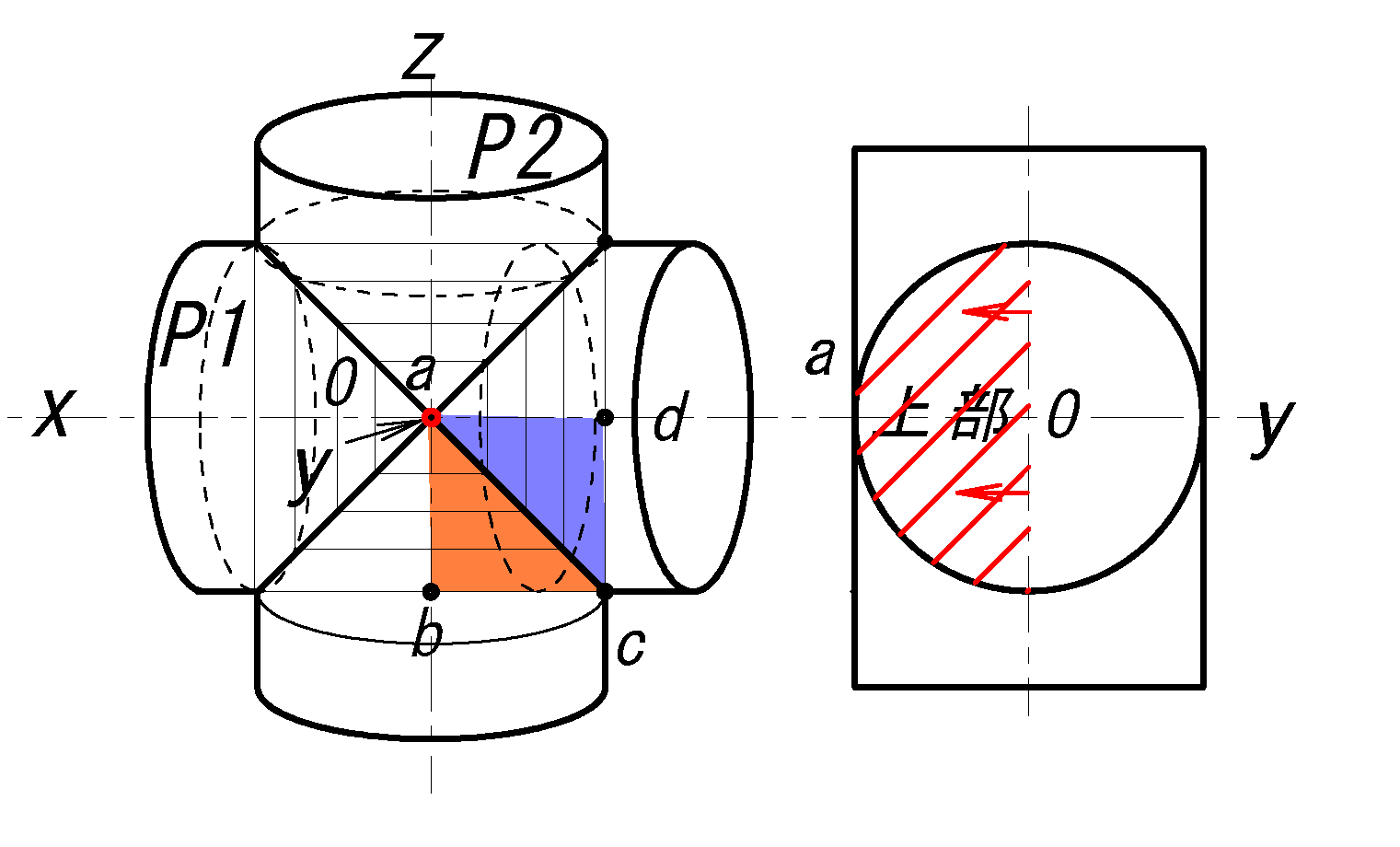
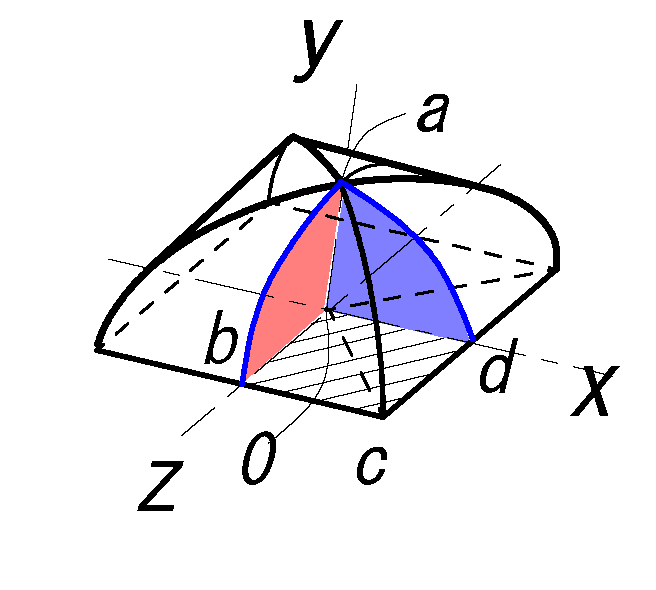
図形としてのV の体積:
\(|V|=\iiint_V \chi_{V} dx dy dz=\iiint_V 1 dx dy dz\)
V が体積確定(体積をもつ)とはこの積分ができることである。
V の体積を\(|V|\)で表す。
積分領域(立体):
\(V=\{(x,y,z)|x^2+y^2=r^2\) \(\ ,\ y^2+z^2=r^2 \}\)
積分領域(平面):
\(D=\{(x,z)|0\le x\le \sqrt{r^2-y^2}\) \(\ , 0\le z\le \sqrt{r^2-y^2}\}\)
\(V_0=\dsiii_V dx dy dz\)
\(=\dsi_y \left( \dsii_D dx dz \right) dy \)
\(=\dsi_0^r \left( \dsi_0^{\sqrt{r^2-y^2}}dx \dsi_0^{\sqrt{r^2-y^2}} dz\right) dy\)
\(=\dsi_0^r dy \dsi_0^{\sqrt{r^2-y^2}} \sqrt{r^2-y^2} dx\)
\(=\dsi_0^r dy \left[{\sqrt{r^2-y^2}}x\right]_0^{\sqrt{r^2-y^2}}\)
\(=\dsi_0^r (r^2-y^2)dy\) \(=\left[r^2y- \frac{r^3}{3}\right]_0^r= \frac{2r}{3}\)
\(\therefore 答: \underline{ 8V_0=8\displaystyle\frac{2r}{3}=\displaystyle\frac{16}{3}r^3 }\)
・3つの接ベクトルが張るのが平行6面体です。
・3つのベクトルの「スカラーの3重積」の計算から平行6面体の体積が求まる。
【参考先】
スカラーの3重積の式は「\((\b{a} \x \b{b})\cdot \b{c}\)」です。(下図)
(ベクトルa,b の外積、これとベクトルC との内積)
・またスカラーの3重積は3つのベクトルの行列式に等しい。
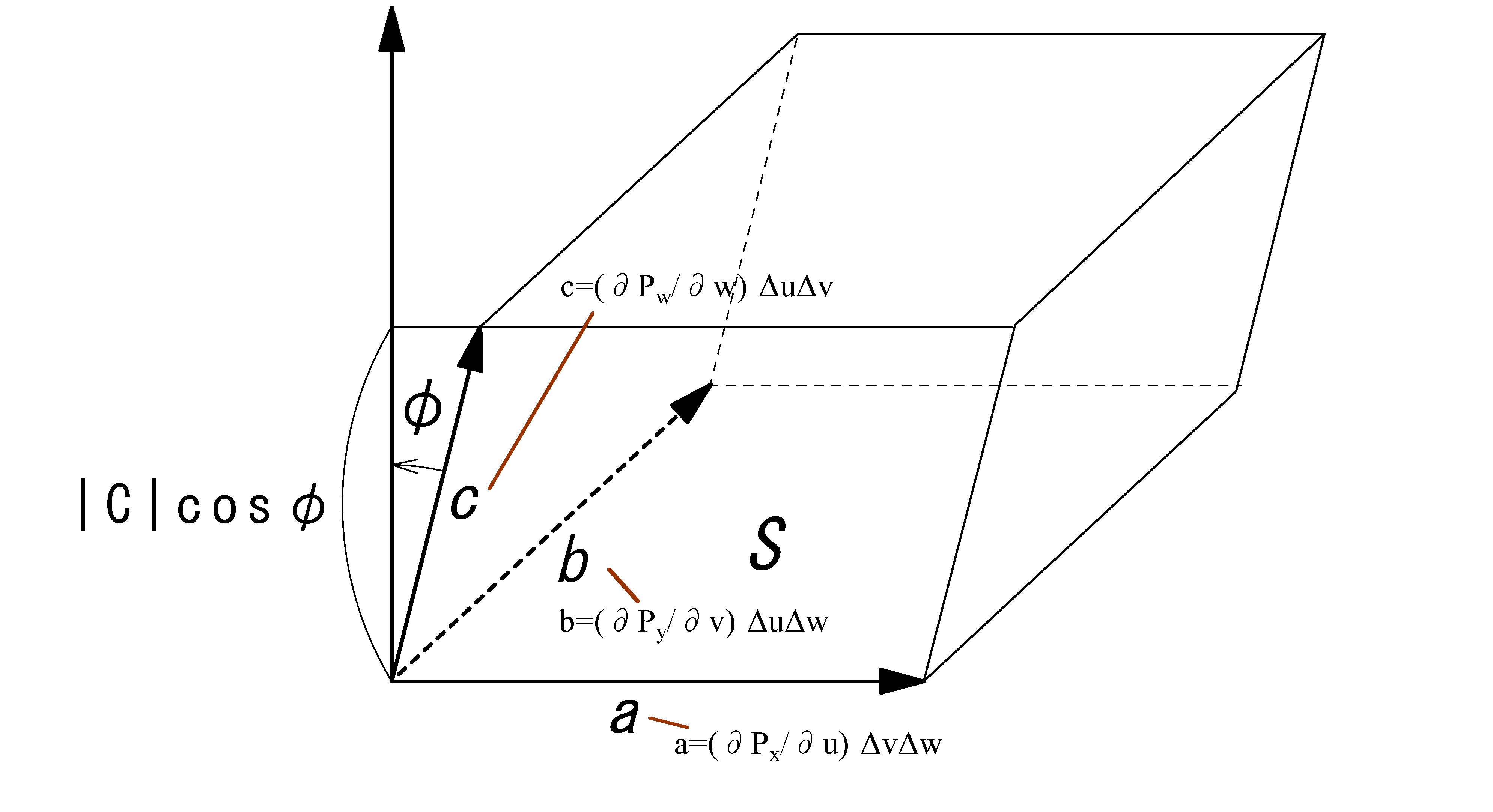
\(P_u= \begin{pmatrix} \pder{p_x}{u}\\ \pder{p_y}{u}\\ \pder{p_z}{u} \end{pmatrix}\) \(\, \) \(P_v= \begin{pmatrix} \pder{p_x}{v}\\ \pder{p_y}{v}\\ \pder{p_z}{v} \end{pmatrix}\) \(P_v= \begin{pmatrix} \pder{p_x}{w}\\ \pder{p_y}{w}\\ \pder{p_z}{w} \end{pmatrix}\)
\(V'=|P_u\ ΔvΔw\ \ P_v\ ΔuΔw \ \ P_w\ ΔuΔv|\)
次式の例えば、 \(p_{xu}=\pder{p_x}{u}\)\(\ ,\) \(p_x=x(u,v,w)\) です。\(= \begin{vmatrix} p_{xu}\ ΔvΔw & p_{xv}\ ΔuΔw & p_{vw}\ ΔuΔv\\ p_{yu}\ ΔvΔw & p_{xv}\ ΔuΔw & p_{vw}\ ΔuΔv\\ p_{zu}\ ΔvΔw & p_{zv}\ ΔuΔw & p_{zw}\ ΔuΔv \end{vmatrix}\)
上式を展開して、共通因子(実数)は行列式の外にだせる。
\(=
\begin{vmatrix}
p_{xu}& p_{xv}& p_{vw}\\
p_{yu}& p_{xv}& p_{vw}\\
p_{zu}& p_{zv}& p_{zw}
\end{vmatrix}\)
\(ΔuΔvΔw\)
\(=\color{red}{J}\ ΔuΔvΔw\)
\(J= \begin{vmatrix} p_{xu}& p_{xv}& p_{vw}\\ p_{yu}& p_{xv}& p_{vw}\\ p_{zu}& p_{zv}& p_{zw} \end{vmatrix}\) \(= \begin{vmatrix} \pder{p_x}{u}& \pder{p_x}{v}& \pder{p_x}{w}\\ \pder{p_y}{u}& \pder{p_y}{v}& \pder{p_y}{w}\\ \pder{p_z}{u}& \pder{p_z}{v}& \pder{p_z}{w} \end{vmatrix}\) ⓐ
つぎの関係があるから;
\(\Phi(u,v,w)\)\(=\left(x(u,v,w),y(u,v,w),z(u,v,w) \right) \)
\(=(p_x(u,v,w),p_y(u,v,w),p_z(u,v,w))\)
\(p_{xu}=\pder{p_x}{u}=\pder{x}{u}=x_u\)
ⓐ \(= \begin{vmatrix} \pder{x}{u}& \pder{x}{v}& \pder{x}{w}\\ \pder{y}{u}& \pder{y}{v}& \pder{y}{w}\\ \pder{z}{u}& \pder{z}{v}& \pder{z}{w} \end{vmatrix}\) \(= \begin{vmatrix} x_u& x_v& x_w\\ y_u& y_v& y_w\\ z_u& z_v& z_w \end{vmatrix}\)
…導出終了。
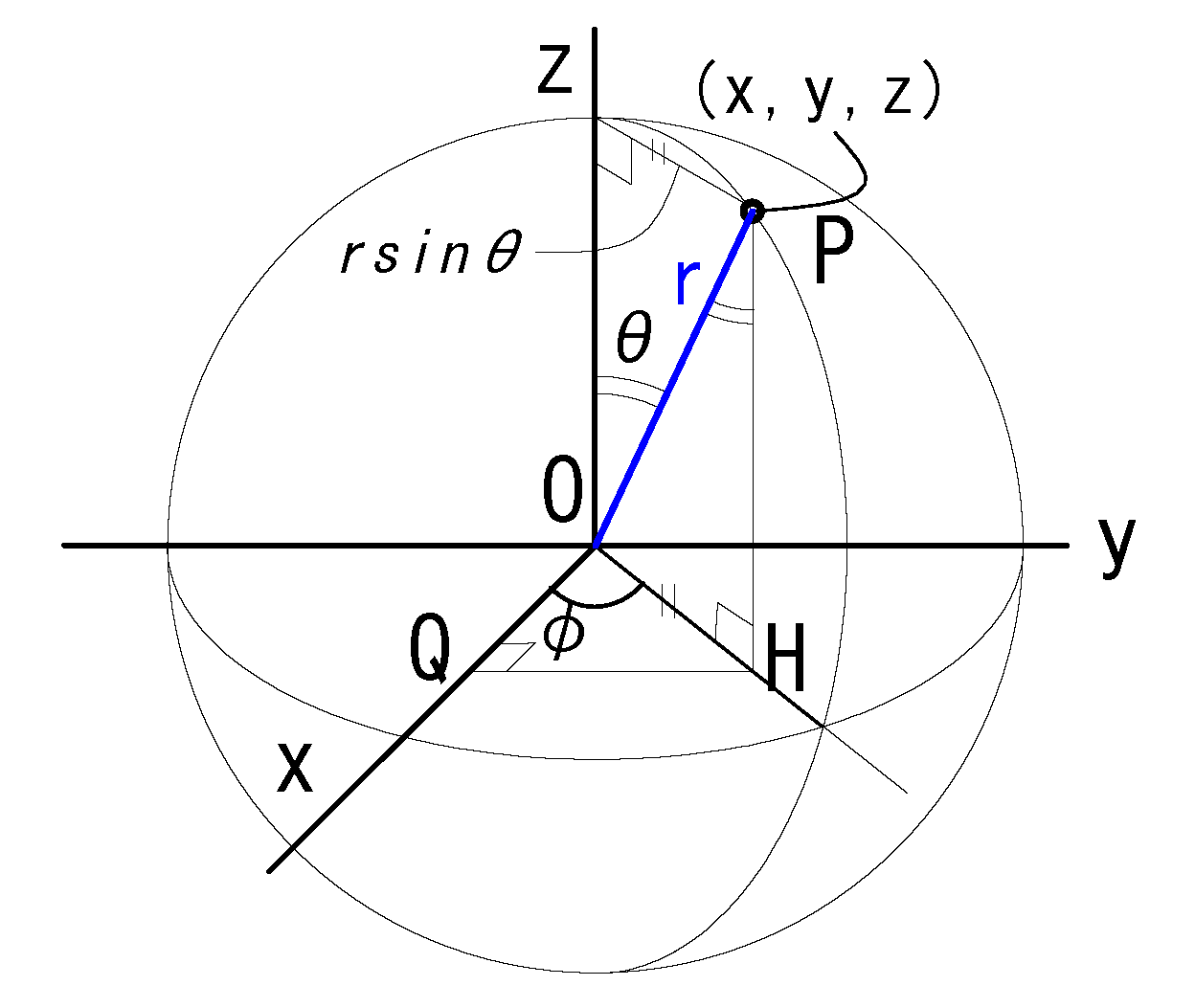
•\(x=r sin\theta cos\varphi=α\) \( \ \)
\(y=r sin\theta sin\varphi=β\) \( \ \)
\(z=r cos\theta=γ \)
•\((0\le θ \le \pi )\) \(,\) \(( 0\le φ \le 2\pi )\)
\( \dsiii_V\ f(x,y,z)\ dxdydz\)\(=\dsiii_{V'}\ f(α,β,γ) r^2\ sinθ\ dr\ dθ\ dφ\) \(\ :❽\)
\(( f(α,β,γ)\) \(=f(r sin\theta cos\varphi,\ r sin\theta sin\varphi,\ r cos\theta) )\)
\( \dsiii_V z\ dx\ dy\ dz\)
\(V=\{(x,y,z)|\color{red}{ x^2+y^2+z^2 \le 1} \}\)
極座標と直交座標の変換式:
\(x=r sin\theta cos\varphi\) \( \ \)
\(y=r sin\theta sin\varphi\) \( \ \)
\(z=r cos\theta \)
\(V'=\{(x,y,z)| 0\le r \le 1,\ 0\le θ \le \pi \)\(,\) \( 0\le φ \le 2\pi \} \)
\( \dsiii_V\ f(x,y,z)\ dxdydz\)
\(=\dsiii_{V'}\ z\ \underline{|J|}\ sinθ\ dr\ dθ\ dφ\)
\(=\dsiii_{V'}\ z\ \underline{r^2\ sinθ} \ dr\ dθ\ dφ\)
\(=\dsiii_{V'}\ r cosθ\ r^2\ sinθ\ dr\ dθ\ dφ\)
\(=\dsi_0^a r^3 dr \dsi_0^\pi \color{red}{sinθ cosθ} dθ \dsi_0^{2\pi} dφ \)
\(sinθ cosθ=\frac{1}{2} sin2θ\)だから
\(=\left[\displaystyle \frac{1}{4}r^4 \right]_0^1 \)
\(\cdot \displaystyle \frac{1}{2}\left[-\displaystyle \frac{1}{2} cosθ \right]_0^{\pi}\)
\(\left[ φ \right]_0^{2 \pi}\)
\(=\frac{1}{4} \cdot -\frac{1}{4}[-2] \cdot [2 \pi] \)
\(=\displaystyle \frac{1}{4}\pi\)
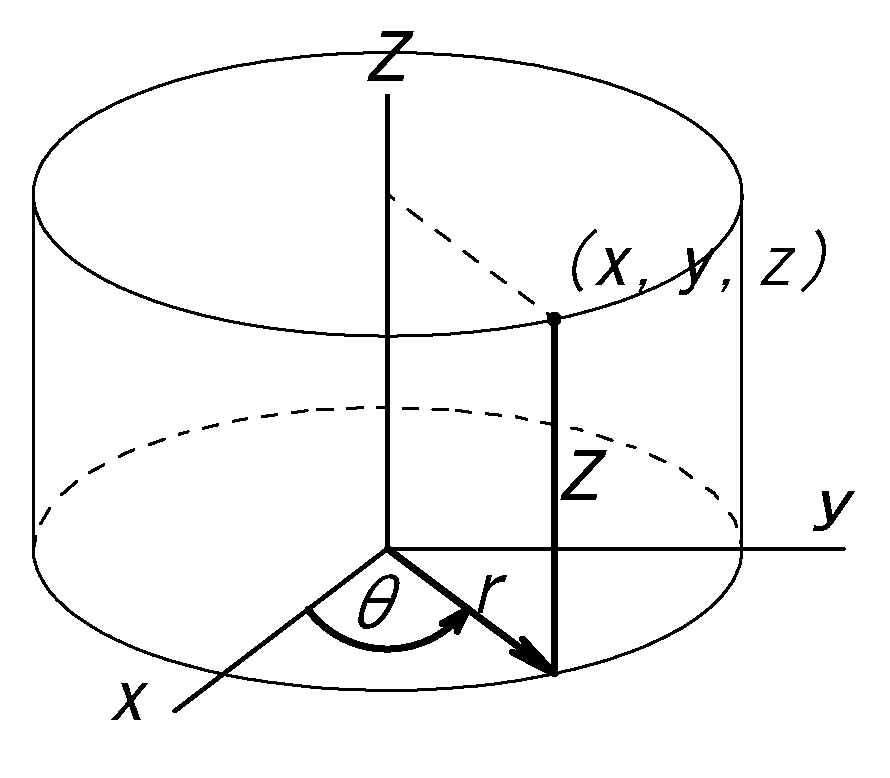
\(x=rcosθ\)\(,\ y=rsinθ\)\(,\ z=z\)
\(0 \le r\) \(\ ,\ \)\(0\le θ \le 2\pi \)
