|
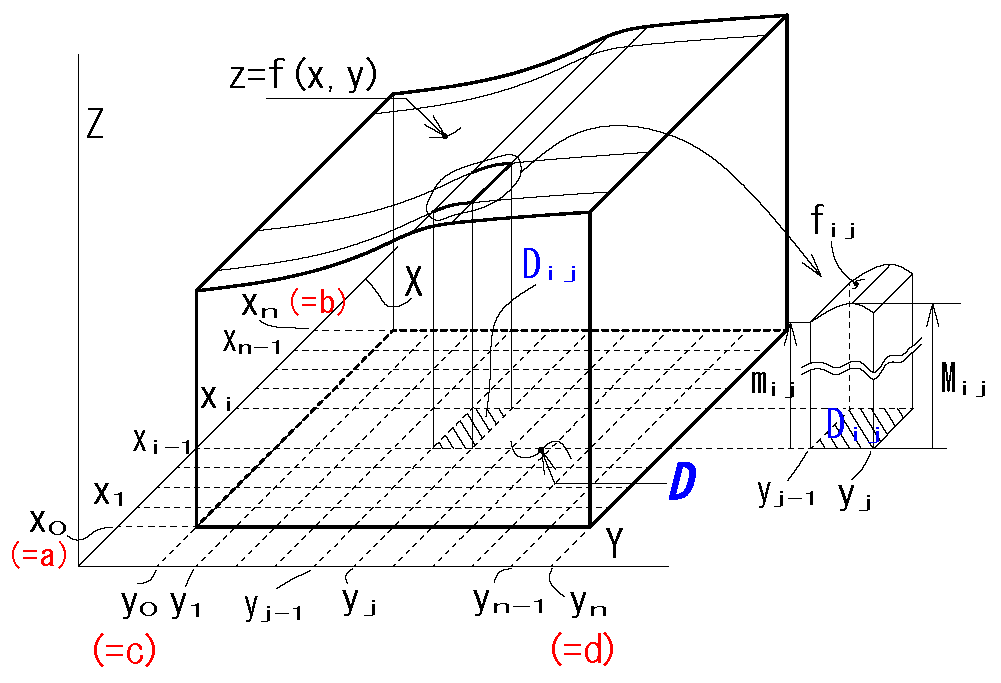
【重積分の定義】
積分領域\(D\)は 有界閉区間。
また \(f(x,y)\) は\(D\)上で有界な関数とする。
\(f(x,y)\)の上積分と下積分が等しいとき: \(f(x,y)\) はリーマン積分において可積分である。 この積分を重積分(2重積分)といい、 \( \iint_D f(x,y) dxdy\) と表す。すなわち次の関係がある。 \( \iint_D f(x,y) dxdy\) \(=\overline{\iint}_D f(x,y) dxdy\) \(=\underline{\iint}_D f(x,y) dxdy\) |
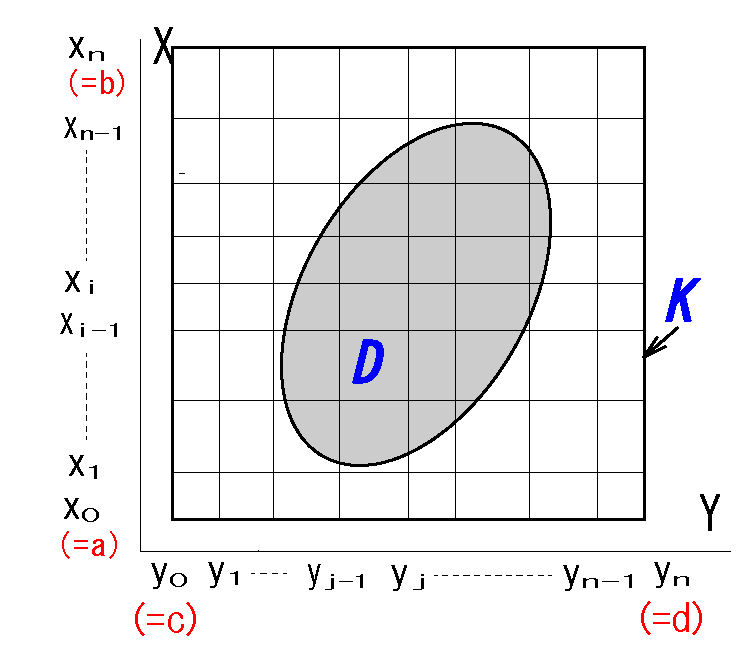
以下は特性関数 \(\chi_{D}\) の定義です:
\(
\begin{eqnarray}
\chi_{D}(x,y)=
\begin{cases}
1\ :((x,y) ∈ D) ※1 \\
0\ :((x,y) ∈ K \setminus D)※2
\end{cases}
\end{eqnarray}
\)
(\(K \setminus D\): \(\ K \)と\(D\)の差集合 )
集合の記号はここを参照【参照先】
☞※1:(x,y) が領域D にあるとき
☞※2:(x,y) が領域D 以外の\(K\)平面にあるとき
この関数の出力は「1」「0」に注目し、仮に\(\chi_{D}=1\)なら
\( \chi_{D} \times 面積 D =面積 D \)
高さ1 とは、D は体積でもあるが面積でもある。
\(|D|=\dsii_K \chi_{D} dx dy=\dsii_D 1 dxdy\)
D が面積確定(面積をもつ)とはこの積分ができることである。
D の面積を\(|D|\)で表す。
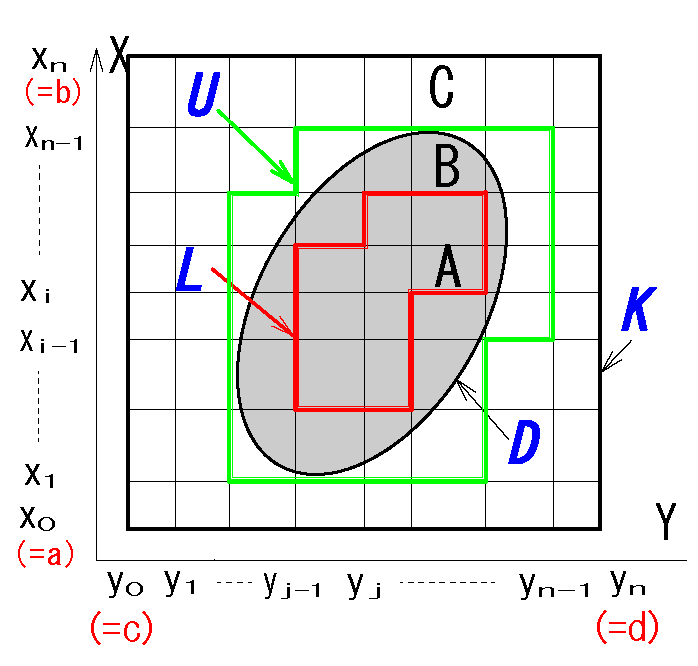
上図の説明:
・ユークリッド平面 \(\b{R}^2\)において
D:有界閉集合、K:有界閉集合、\( D ⊂K\)
・マス目を細かくしていくとL とU が近づいていく。
【復習】
記号 \(\cap\) は積集合であり、また共通部分ともいう。
さらに以下を示すこともある。
\(A \cap B \neq 0\):集合A とB は交わる。
\(A \cap B = 0\):集合A とB は交わりはない。
\(\chi_{D}\) の有界閉集合D の上積分\(\overline{U}\)のことをいう。
(D の面積を外側から測るイメージ)
\(\chi_{D}\) の有界閉集合D の下積分\(\underline{L}\)のことをいう。
(D の面積を内側から測るイメージ)
|D|を有界閉集合の面積とすると:
\(L(\chi_{D},\Delta)≤|D|≤U(\chi_{D},\Delta)\)
の関係がある。そして
\(\underline{L}(\chi_{D},\Delta)=\overline{U}(\chi_{D},\Delta)\)
のとき
\(B\)
はジョルダンの面積確定(area fixed)という。
