\( \require{cancel} \)

earth

湘南理工学舎

[戻る] 　　
2023/03/10 　　
2020/02/06

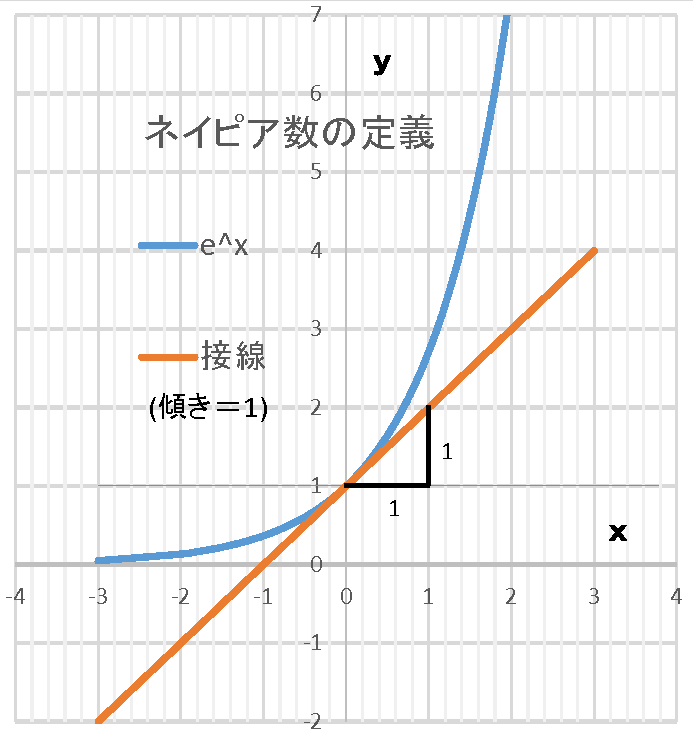
ネイピア数の導関数

--目　次--

1.ネイピア数について 2.ネイピア数 e の定義式1
3.ネイピア数 e の定義式2 4.\(e^x\) の導関数を求める
5.同値な定義式の証明
6.例題1 \(\displaystyle \lim_{ n \to \infty} \left ( \frac{n+3}{n}\right )^{n+1}\) 例題2 \(\displaystyle \lim_{ n \to \infty} \left (1-\frac{1}{n}\right )^{n}\)
7.指数・対数関数の極限
【閑話】世界で一番美しい数式…

1.ネイピア数について
ネイピア数 e は自然対数の底などとして様々な場面（数学、物理、化学など）に次の様な形でてくる数です。

\(e=2.718 \cdots　, \) \(\quad e^x \ ,\) \( \quad log_e x=ln\ x \)

微分しても変わらないという不思議・特別な数です。

そこで、他と独立して専用のページにしました。

今回はネイピア数 e の概念を述べ、ネイピア数 e　の導関数を求めることを目的とします。

2.ネイピア数 e の定義式 1

\( \displaystyle \lim_{ n \to \pm \infty} \left ( 1+ \frac{1}{n} \right )^n　=e \) \( \quad (1)\)

「有界性と収束」の講義において、この式（無限級数）は上に有界な単調増加数列であり、収束する数列であること学びました。

この式はネイピア数 e の定義の式、そのものです。

この式の収束値はネピア数です。
（はじめは複利計算のために使ったそうです）

式(1) と同値な定義式があります。…以下に示します。

\( \displaystyle \lim_{ x \to \pm\infty} \left ( 1+ \frac{1}{x} \right )^x =e\) \( \quad (1)'\)

\( \displaystyle \lim_{ x \to 0} \left ( 1+ x \right )^\frac{1}{x}=e \) \( \quad (1)''\)

上式はあとで証明します。

\( \displaystyle \sum_{n=0}^{\infty} \frac{1}{n!}=e\) \( \quad (1)'''\)

3.ネイピア数 e の定義式 2

あと一つの定義式は：

\( \displaystyle \lim_{ h \to 0} \frac{e^h -1}{h} =1 \) \( \quad (2)\)

指数関数（ \(y=a^x\) ）を考え、この関数 x=0 での微分係数が 1 となるときの底をネピア数 e と定義している。

\( f'(0)=\displaystyle \lim_{ h \to 0} \frac{ f(0+h)-f(0) }{h}\) \(= \displaystyle \lim_{ h \to 0} \frac{ (a^h-1) }{h}\)

以下のような対応になっている。
\( \frac{ (a^h-1) }{h} \longrightarrow \frac{e^h -1}{h} =1 \)

当然だが式(2)から式(1)を導き出すこともできます。

　　

ネイピア数

fig1　　ネイピア数の定義

　　

4. \( e^x　\) の導関数を求める

\( f'(x)=(e^x)'= \displaystyle \lim_{ h \to 0} \frac{f(x+h)-h(x)}{h}\) \(=\displaystyle \lim_{ h \to 0} \frac{(e^{x+h} -e^x)}{h}\)

\(=\displaystyle \lim_{ h \to 0} \frac{e^x (e^{h} -1)}{h}\)

\(= e^x \underline{ \left( \displaystyle \lim_{ h \to 0} \frac{(e^{h} -1)}{h} \right) } \)❶

以下に下線部を求めます。

上記の公式 (1)''
\( \displaystyle \lim_{ x \to 0} \left ( 1+ x \right )^\frac{1}{x}=e \ \) (※1-1)

両辺の対数をとる
\( log\ \left [ \displaystyle \lim_{ x \to 0} \left ( 1+ x \right )^\frac{1}{x}\ \right ] =log\ e \)

\( \displaystyle \lim_{ x \to 0}\ log\ \left [ \left ( 1+ x \right )^\frac{1}{x}\ \right ] =1 \)

\( \displaystyle \lim_{ x \to 0}\ \left ( \frac{log\ ( 1+ x )}{x} \right ) = 1 \ \) (※1-2)

ここで、　 \( e^u=1+x \longrightarrow x=e^u-1 \)　として

さらに、　 \( x　\rightarrow　0 \)　のとき \( u　\rightarrow　0 \)

\( \displaystyle \lim_{ x \to 0}\ \left ( \frac{log\ ( 1+ x )}{x} \right )\)

\(=\displaystyle \lim_{ u \to 0}\ \left ( \frac{log\ (e^u )}{(e^u-1)} \right )\) \(=\displaystyle \lim_{ u \to 0}\ \left ( \frac{ u\ log\ (e)}{(e^u-1)} \right )\) \(=\displaystyle \lim_{ u \to 0}\ \left ( \frac{ u\ \cdot 1 }{(e^u-1)} \right )\)

\( \therefore \displaystyle \lim_{ u \to 0}\ \left ( \frac{ u }{e^u-1} \right )=1\)

この両辺の逆数をとる
\( \displaystyle \lim_{ u \to 0}\ \left ( \frac{e^u-1}{u} \right )=1\)

さらに \(u \rightarrow x \rightarrow h \) に変える。
\( \underline{ \displaystyle \lim_{ x \to 0}\ \left ( \frac{e^x-1}{x} \right )=1 } \ \) (※1-3)

\( \underline{ \displaystyle \lim_{ h \to 0}\ \left ( \frac{e^h-1}{h} \right )=1 } \)

　　　　

❶ \(= e^x \underline{ \left( \displaystyle \lim_{ h \to 0} \frac{(e^{h} -1)}{h} \right) }\)

\(= e^x \cdot 1 = e^x\)

\( \therefore (e^x)'=e^x \) 　…微分公式

また \( { \displaystyle \lim_{ h \to 0}\ \left ( \frac{e^h-1}{h} \right )=1 } \)

は公式(2)と同じです。
すなわち❶を求めたことは公式(1)’’から公式(2) を導出したことになります。

以下は忙しい人はパスしてもよいでしょう！

5. 同値な定義式(1)と公式(1)'の証明
\( \displaystyle \lim_{ n \to \infty} \left ( 1+ \frac{1}{n} \right )^n=e \) \( \quad (1)\)

\( \displaystyle \lim_{ x \to \infty} \left ( 1+ \frac{1}{x} \right )^x=e \) \( \quad (1)'\)

\( n:自然数　x：実数 \) の違い、離散的（ステップ）変化する自然数と連続区的に変化する実数の違いです。
実数 x は自然数 n と n+1 の間にあるとします。
•\( n≤x<n+1 \) の関係があります。
ごれの逆数をとると：
\(　(\frac{1}{n+1})<(\frac{1}{x})≤(\frac{1}{n})\)　

上式の各項に「1」をくわえると
• \(　(1+\frac{1}{n+1})<(1+\frac{1}{x})≤(1+\frac{1}{n})\)　

これより
\(　\underbrace{(1+\frac{1}{n+1})^n}_{ ❸ }<(1+\frac{1}{x})^x ≤\underbrace{(1+\frac{1}{n})^{n+1}}_{ ❹ } \)　

❸、❹　の n が無限大の極限値は e に収束します。
❸ \(= \frac{ (1+\frac{1}{n+1})^{n+1} } { (1+\frac{1}{n+1})^x} = \frac{e}{1}=e \)

❹　 \(= ((1+\frac{1}{n})^{n}) (1+\frac{1}{n+1}) = e \cdot 1 =e \)

従って、はさみうちの原理より式(1)' が成り立ちます。

6.例題
例題1：次の極限値を求めよ
\(\displaystyle \lim_{ n \to \infty} \left ( \frac{n+3}{n}\right )^{n+1}\)

ヒント: \(\displaystyle \lim_{ n \to \infty} \left ( 1+ \frac{1}{n} \right )^n=e \) を使う。

次のように展開していきます。

\( \left ( \frac{n+3}{n} \right ) ^{n+1} \) \( = \left ( 1+ \frac{3}{n} \right )^{n+1} \) \( = \left ( 1+ \frac{1}{\frac{n}{3}} \right )^{n+1} \)

ここで、 \(N=\frac {n}{3} \quad n=3N \) とおく。
\( = \left ( 1+ \frac{1}{N} \right )^{3N+1} \)

\( = \left ( 1+ \frac{1}{N} \right )^{3N} \left ( 1+ \frac{1}{N} \right ) \)

\( = \left [ \left ( 1+ \frac{1}{N} \right )^N \right ] ^{3} \left ( 1+ \frac{1}{N} \right ) \)

これより与式は：

\(\displaystyle \lim_{ n \to \infty} \left ( \frac{n+3}{n}\right )^{n+1}\) \( = \displaystyle \lim_{ n \to \infty} \left [ \left ( 1+ \frac{1}{N} \right )^N \right ] ^{3} \left ( 1+ \frac{1}{N} \right ) \)

\( =　\left [ \displaystyle \lim_{ n \to \infty} \left ( 1+ \frac{1}{N} \right )^N \right ] ^{3} \left ( 1+ \frac{1}{N} \right ) \)

\( \underline{ = e^3 \cdot 1 =e^3 }\)

となりました。（関数電卓、エクセルなどで確かめて下さい！）

例題2：次の極限値を求めよ
\(\displaystyle \lim_{ n \to \infty} \left (1-\frac{1}{n}\right )^{n}\)

\(t=-n\) として　\([n \to \infty]\) ⇔\([t \to -\infty]\)
与式\(=\displaystyle \lim_{ t \to -\infty} \left (1+\frac{1}{t}\right )^{-t}\) \(=\displaystyle \lim_{ t \to -\infty} \left\{ \left (1+\frac{1}{t}\right )^{t}\right\}^{-1}\)
\(=e^{-1}\)

7. 指数・対数関数の極限
以下の式は教科書によっては「指数・対数関数の極限の公式」になっているのでまとめておきます。
上記の4項「4.\(e^x\) の導関数を求める」のなかの式（(※1-2)、(※1-3)、(※1-3)）です。

\( \displaystyle \lim_{ x \to 0} \left ( 1+ x \right )^\frac{1}{x}=e \ \) (※1-1)

\( \displaystyle \lim_{ x \to 0}\ \left ( \frac{log\ ( 1+ x )}{x} \right ) = 1 \ \) (※1-2)

\( \displaystyle \lim_{ x \to 0}\ \left ( \frac{e^x-1}{x} \right )=1 \ \) (※1-3)

coffe

[コーヒーブレイク/閑話］…お疲れさまでした

【参考図書】Newton　「数学のせかい　教養編」
世界で一番美しい数式と言われている式
それがオイラーの等式です。

\( e^{i π}+ 1 ＝ 0 \)

この式には「いわくありげ」な不思議な数が集まっています、まず、その演算結果が0（ゼロ）です。
0 は足し算/引き算では影響しない数。
1 はかけ算/割り算では影響しない数。
\(π\ \)は　3.14159 …の無限小数
\(e\ \)は 2.71828 …の無限小数
\(e^x\) は何回微分しても変わらない。（\(e^x\)のまま）
上の簡単な式により、虚数を通して、このような複雑な、「いわくありげ」な数の演算結果が0（ゼロ）になる。
虚数も長年否定されきた、２乗するとマイナスになる数。
英語ではimaginary number である。　
0（ゼロ）も過去に長年、数字として認められなかった歴史があります。

この式の導出は次の通りです。
オイラーの公式：
\( e^{iθ}=cos\ θ+i\ sin\ θ\ \)

この式に \( θ=π \) を代入する。
\( e^{iπ}=-1+0=-1\ \)

\( \therefore e^{i π}+ 1 ＝ 0 \)

　

　