x は弧度法(ラジアン)の値です。
\( 0 <x\ <\ \frac{π}{2}\)
:x の定義域
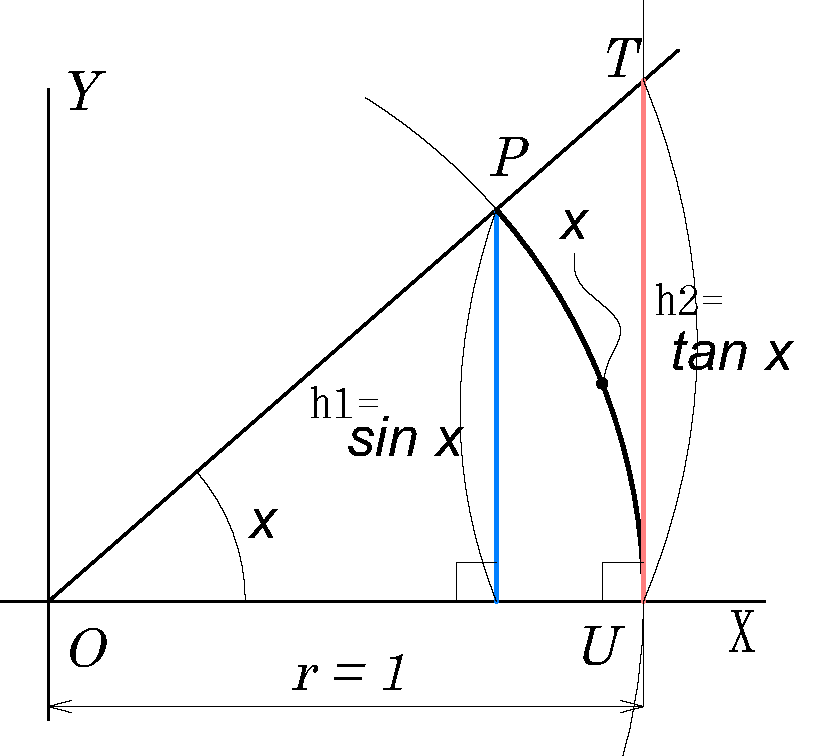
図は半径 r = 1 の単位円です。(半径 1 がポイント)
図を参照して極限を求めるための準備をします。
•円弧PUの長さ:
\(=\stackrel{ \Large \frown }{ PU }=x \)
\(\quad \because 2\ π r\ \frac{x}{2π} = x\) (r=1)
•\(h1=r\ sin\ x=sin\ x\)
•\(h2=r\ tan\ x=tan\ x \)
•面積△OPU:
\(\quad= \frac{1}{2} r\ sin\ x = \frac{sin\ x}{2} \)
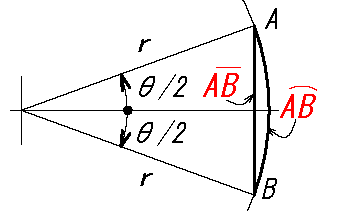
•面積 扇形OPU:
\(=π r^2 \frac{x}{2π}=\frac{x}{2}\)
•面積△OTU:
\(= \frac{1}{2} r\ tan\ x = \frac{tan\ x}{2} \)
以上の計算は単位円の半径 r=1 の恩恵により 簡潔な式になりました。
…これで準備ができました。
これから右側極限値を求めます。
この結果より次の3つの面積を比較します。
△OPUの面積 < 扇形OPUの面積 < △OTUの面積
\( \frac{sin\ x}{2}\)\(< \frac{x}{2}\) \(< \frac{tan\ x}{2} \)
この式に
\( \frac{2}{sin\ x}\)を掛ける。
\(1 < \frac{x}{sin\ x}< \frac{1}{cos\ x}\)
逆数をとる(不等号が逆に)
\( 1 > \frac{sin\ x}{x}> cos\ x \)
整理して書き換える。
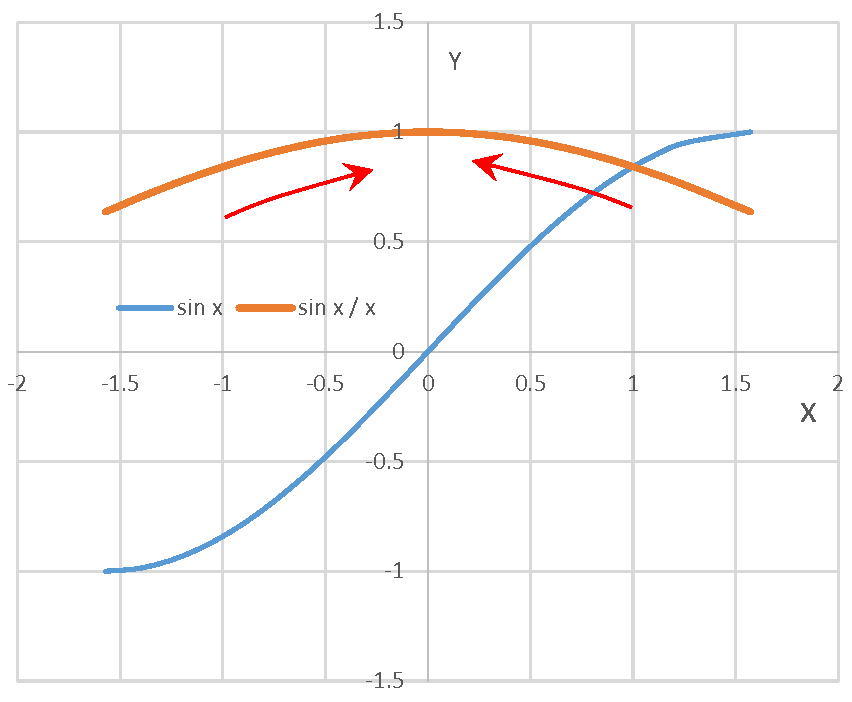
\( cos\ x < \frac{sin\ x}{x}< 1 \)
\(x \rightarrow 0 \)
での極限では最右辺と最左辺は
「1」です。はさみうちの原理より
\(\displaystyle \lim_{ x \to +0}\frac{sin x}{x}\ =1 \)
\( \quad (1)\)
上記は右側極限値です。
\( -\frac{π}{2}< x\ <0\ \)
:x の定義域
\( x=-t \)
とおく、そうすると、表示は「プラス x」は「マイナス t」に変わる。
\( 0 < t <\frac{π}{2} \)
となる。
\(\frac{sin x}{x}= \frac{sin(-t)}{-t}\)\(=\frac{-sin\ t}{-t}\)\(=\frac{sin\ t}{t}\)
\(\displaystyle \lim_{ -x \to 0}\frac{sin x}{x}\ \)
\(=\displaystyle \lim_{ t \to 0}\frac{sin(-t)}{-t}\ \)
\(=\displaystyle \lim_{ t \to 0}\frac{sin\ t}{t}=1 \)
\( \quad (1)' \)
\( \therefore (1)右側極限=(1)'左極限\)
結 論:
\( \underline{ \displaystyle \lim_{ x \to 0}\frac{sin\ x}{x}=1 }\)
\(\quad (2) \)