\( \displaystyle \lim_{ x \to a } f(x)=f(α)\)
関数の連続とは関数が \(x_1=a \) で上式が成り立つときです。
これを連続関数といいます。
イメージ的に一様連続とはもっと厳しい条件になります。
いま、x=a で連続であるといいましたが、一様連続は x が \(x_1=a \) に依らず、どこでも連続であることです。
これを
一様収束とまたは一様連続といいます。また定義域を限定して連続であれば
各点連続という。
一般の連続とは各点連続のことをいっている。
一様収束はx に依存せず、x のどこでも一様の速さで収束する意味です。
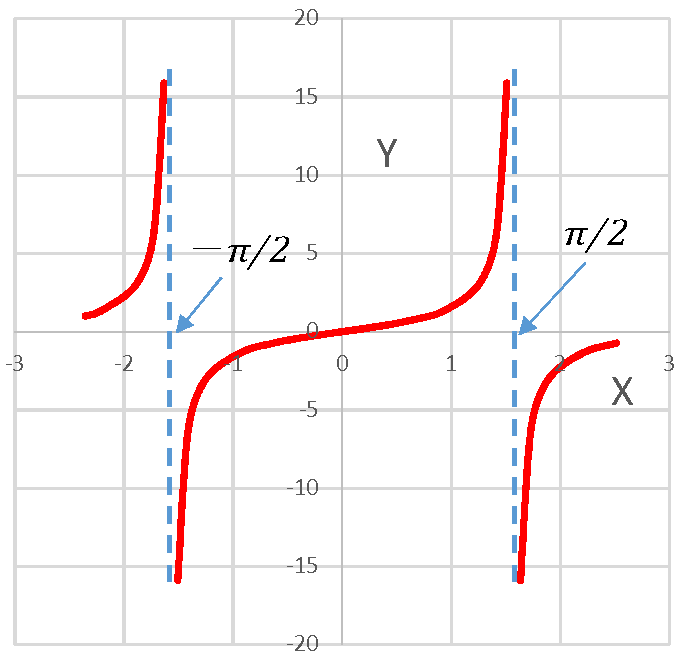
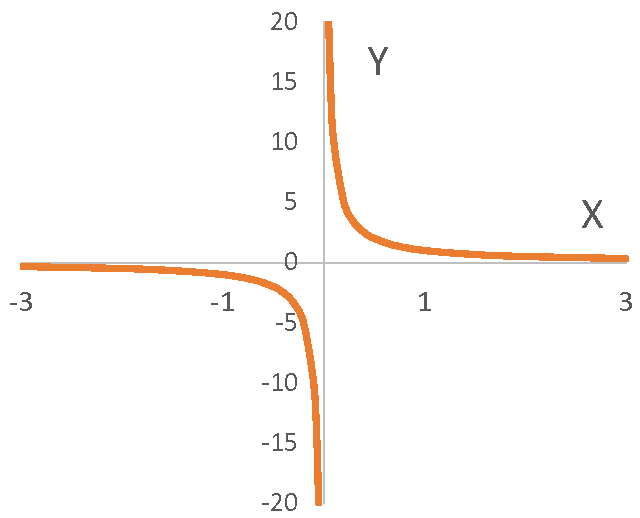
例えば \( f(x)=x^2 \) などは x が十分大きいとき、x の微小な変化でも f が猛烈に変化する。
\( tan\ x \), \( \quad \frac{1}{x}\) …
このような関数は一様連続ではありません。
関数が一様連続であれば、連続関数であるが、その逆は成立しない。
ε・δ 論法による連続とは:
ある区間にある a と、任意の ε がある。
\( \forall ε>0, \quad \exists δ \quad s.t.\)
\( 0<|x-a|<δ\) \( \Rightarrow |f(x)-f(a)|<ε \)
ならば x=a において\(f(x)\) は連続である。
ここでは
a に対応する ε と δ がある。
ε・δ 論法による一様連続とは:
任意の ε があり、ある δ がある。
\( \forall ε>0, \quad \exists δ \quad s.t.\)
\( 0<|x_1-x_2|<δ\) \( \Rightarrow |f(x_1)-f(x_2)|<ε \)
ならば \(f(x)\) は一様連続である。
ここでは
a に依存しない ε と δ がある。
論理記号:
•\(\ \forall ε \):「すべてのε (all)」または「任意のε (any)」
•\(\ \exists δ \):「δが存在する (exist)」
•\(\ s.t.A \):「Aのような (such that)」
•\(\ A \Rightarrow B \):「AならBである」
一様に連続であれば、はじめに決めた ε に対して y のどの位置でも
距離 \(|f(x_1)-f(x_2)|\ <ε \)
を満足する一様なδ が存在する。
本題の関数は x を右側(+)から 0 に近付けると f(x) は急激に上昇し 無限大に向かう。
このようは急上昇する領域を考えると:
(x が 0 に近づき、y が急上昇)
距離 \( |f(x_1)-f(x_2)|\ <ε \ \) (※)
を満足するような
距離\(|x_1-x_2| \ <δ \)
はどんどん小さくなり、(※)を満足できる
一様な δ がなくなる。
これより一様連続と同じだが、これを
各点連続である。
同様にして関数
\(y=x^2\) は x の増加に対し y が急上昇するので、一様連続ではないが、定義域を限定すれば一様連続となる。