
(1')\( y=\sin^{-1} \frac{x}{a} \ \)
より一般化した式ができます。(2)\( y=\tan^{-1} x \ \)
\( y=\tan^{-1} x \) とすると\( \ x=\tan y \ \)と表せるので(2')\( \ y=\tan^{-1} 2x \ \)
商の微分を使い解く。(2'')\( \ y=\tan^{-1} \frac{b}{ax} \ \)
合成関数を使い解く
\(u=\frac{b}{ax}\)
とおくと
\(\ u=tan\ y\)
\(\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx} \)
\(\frac{dy}{du}=\frac{1}{ \frac{du}{dy} }\)
\(=\frac{1}{ \frac{1}{cos^2 y} }\)
\(=\frac{1}{ \frac{cos^2y +sin^2y}{cos^2y} }\)
\(=\frac{1}{1+tan^2 y}\)
\(=\frac{1}{1+u^2}\)
\(\frac{dy}{dx}\)\(=\frac{dy}{du} \frac{du}{dx}\)
\(=\underline{ \frac{1}{1+u^2} \cdot (u)' }\)
\(= \frac{1}{1+(\frac{b}{ax})^2} \cdot \frac{-b}{ax^2}\)
\(= \frac{a^2b^2}{b^2+a^2x^2} \cdot\frac{-b}{ax^2}\)
\(\therefore \frac{dy}{dx}= \frac{-ab}{b^2+a^2x^2}\)
(3)\( y=x^{\frac{1}{3}} \ \)
\( \frac{dy}{dx}=\underline{ \frac{1}{3} x^{-\frac{2}{3}} }\)ですが、

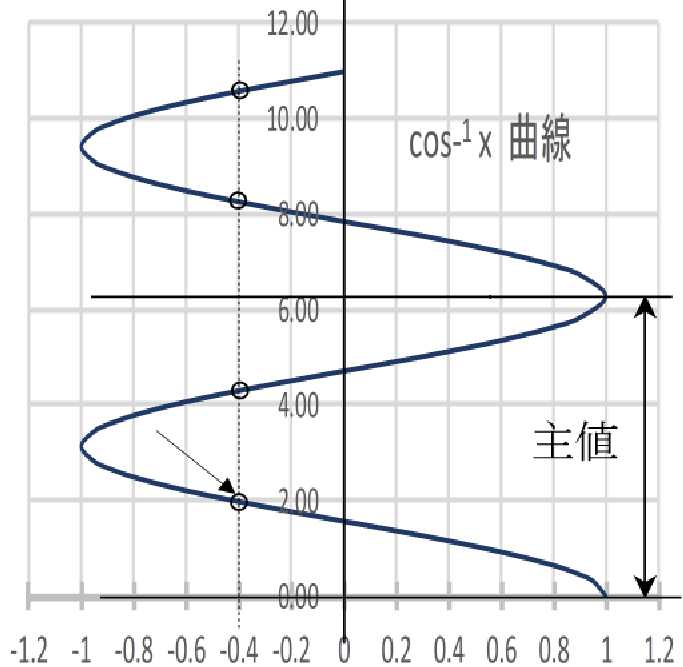
【 \( cos^{-1} \)曲線 x-y(横-縦) 】