楽しく学ぶ…イプシロン・デルタ論法
∗関数の連続・不連続-イメージ図
∗ ε-δ 論法1
∗例題1
∗例題2
∗ε-δ 論法2
∗ε-δ 論法3
∗例題3
∗閑話
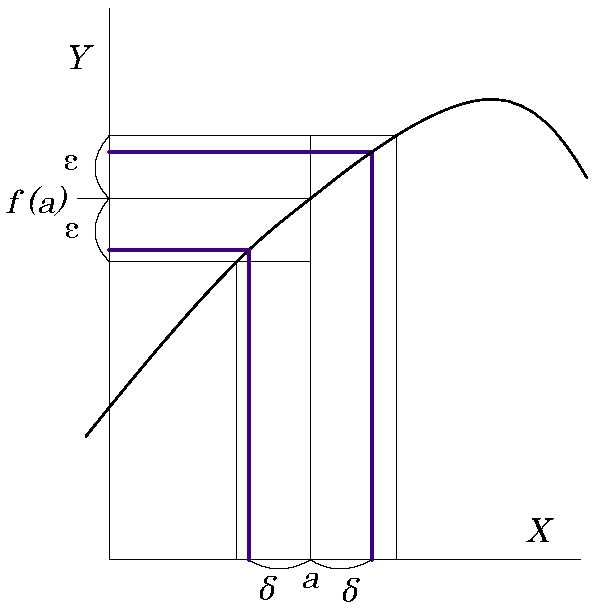
どんなに小さな\(\mathbf{ε}\) にも,対応できる\(\mathbf{δ}\) があること。
(\(\mathbf{ε}\)の指令に\(\mathbf{δ}\)が応えられること。)
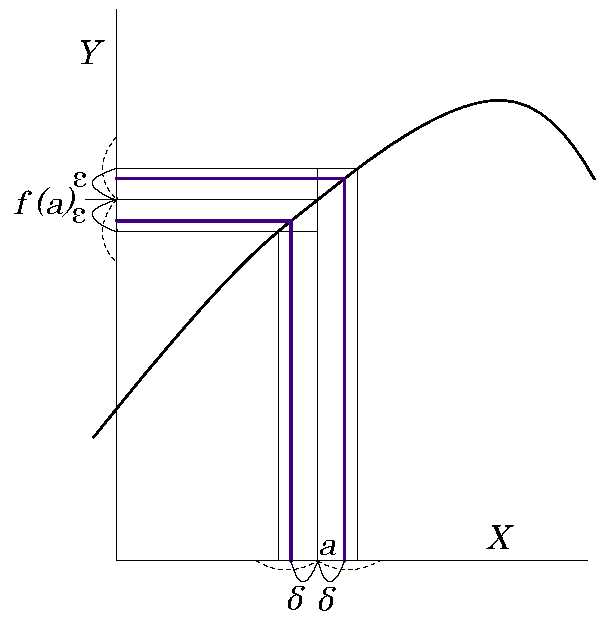
参考に高校での関数の極限の定義は:
x が限りなく a に近づき、f(a)が限りなく\(α\) に近ずくとき、\(α\) を f(x) の極限値という。
\(\displaystyle \lim_{ x \to a} \ f(x)=f(a)=α \) となる。…ことでした。
|
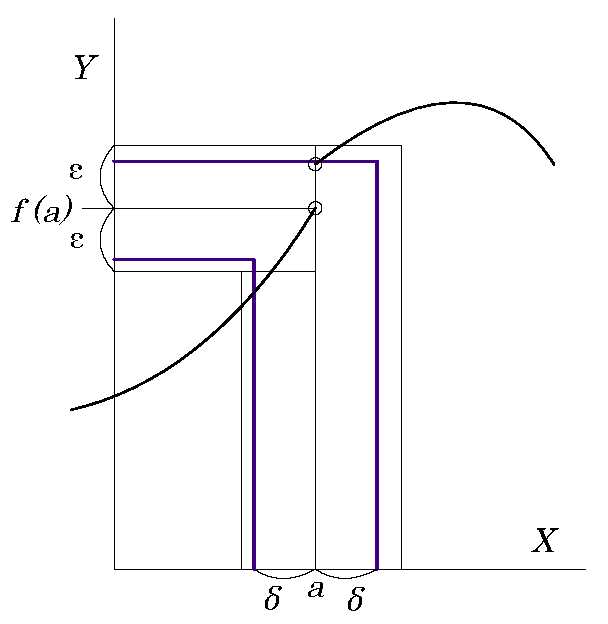
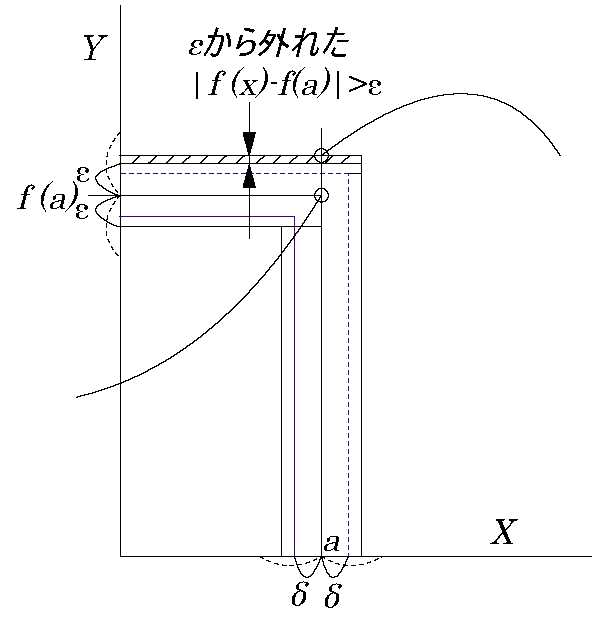
\( \forall ε>0, \quad \exists δ \quad s.t.\) \( \quad 0<|x-a|<δ\) \( \Rightarrow |f(x)-f(a)|<ε \) このとき \(\displaystyle \lim_{ x \to a} \ f(x)=f(a)\) となる。
どんなに小さな正の数\(\mathbf{ε}\)とっても、\(|f(x)-f(a)|<\mathbf{ε}\) となるような
大雑把にいうと: |
論理記号の意味:
•\(\ \forall ε \):「すべてのε (all)」または「任意のε (any)」
•\(\ \exists δ \):「δが存在する (exist)」
•\(\ s.t.A \):「Aのような (such that)」
•\(\ A \Rightarrow B \):「AならBである」
論理記号表記は英文の流れだから、初めて見る日本人は困惑する、慣れるしかないですね!
参考に下の【閑話】に英文の「ε-δ論法」を載せておきました。
注: 「\(0<|x-a|<δ\)」は変数 \(x\) は外側から 「\(a\)に近づが、\(a\)にはならない」を意味する。
|
\( \forall ε>0, \ \exists δ \quad s.t.\) \( \quad 0<\underline{|x-5|}<δ\) \(\ \Rightarrow \ |(2x-5)-5|<ε \) |
|
\( \forall ε>0, \ \exists δ \quad s.t.\) \( \quad 0<\underline{|x-2|}<δ\)\( \Rightarrow |x^2-4|<ε \) |
注(※):2次関数の不等式
\(y=ax^2+bx+c \lt 0\)のときの解:
\(y=0\)のとき \(x=α,\ β\) かつ \(α \lt β\)とすると
解: \(\quad α\lt \color{red}{x\lt β}\)
ε・N 論法では
\( \forall ε>0 \quad \exists N>0 \quad s.t.\ n >N\) \(\ \Rightarrow\ |a_n- α|<ε \)
これにより
\(\displaystyle \lim_{ n \to \infty } a_n= α\)となる。
|
\( \forall ε>0, \quad \exists δ>0 \quad s.t.\)
\( \quad x>δ\ \Rightarrow\ |f(x)-α|<ε \) このとき \(\displaystyle \lim_{ x \to \infty} \ f(x)=α \) となる。
どんなに小さな正の数 ε をとっても \(|f(x)-α|<ε\) となるような \(x>δ\) となる δ が存在すれば |
|
\( \forall ε>0, \quad \exists δ<0 \quad s.t.\)
\( \quad \color{red}{x<δ}\ \Rightarrow\ |f(x)-α|<ε \) このとき \(\displaystyle \lim_{ \color{red}{ x \to -\infty}} \ f(x)=α \) となる。
どんなに小さな正の数 ε をとっても \(|f(x)-α|<ε\) となるような \(x <δ\) となる δ が存在すれば |
