湘南理工学舎・微分積分・イプシロン・エヌ論法1

はじめに

数列の収束の証明 \(ε・N\) 論法について学んでいきます。
本によっては ε・δ 論法（関数の収束も併せた）として扱っていますが、ここでは ε・Ν 論法とします。
以前は微分積分のはじめには必ずイプシロン・エヌ論法の授業がありました。
一見簡単そうで、中に入ると、難解で、難しいと感じる人が多く、微分積分の最初の関門です。
分かり易くをモットーに説明しますので、是非ついて来て下さい!

高校数学での数列の収束は次のような説明でした。
数列\( \{a_n\} \) は \(　n \) を自然数として、次式で表わせる。

\( \{a_n\}=\{\frac{1}{1},\ \frac{1}{2},\ \frac{1}{3},\ …\frac{1}{n},\ …\} \)
（\(\ a_n=\frac{1}{n} \) はこの数列の一般項）

次の式は \(　n \) を無限大にしたとき、\(0\) に収束する式です。
\(\displaystyle \lim_{ n \to \infty } \frac{1}{n}=0 \cdots (1)\)　
高校では、\(　n \) を限りなく大きくしたとき、この数列は限りなく 0 に近づくとして、
\( \{a_n\} \)は 0 に収束し、0 を数列\(　a_n \)の極限値と言いました。
「限りなく近づく」とは直感的、主観的です。
これなら馴れていて分り易いのですが、大学ではそうはいきません。 ε・N 論法が導入されます。

ε・N 論法の定義

\(N\)、\(　n \)：自然数、　\(ε\):実数
任意の正の数 \(ε\) が与えられとき、
\(n≥N\) ならば　\(|a_n-α|<ε　\cdots　(2)　　\)
が成り立つような \(\ N\ \)が、存在するとき、 \(\displaystyle \lim_{ n \to \infty } \ a_n=α \ \) となる。　

・巻末の【閑話】にε-N 論法の英語版を記載しておきました。英語版を大雑把に見ると上の内容は英語版の流れになっている。
（だから、初めて見たとき違和感があるのかなと思う。）
・曖昧さがなく厳密・簡潔すぎて、難しいですね！

ε・N 論法の解説

\(ε\) は小さな数です。（式(2)の意味するところ）
\(\because \)\( \ ε \)（error）は\(a_n\)と\(\ α\ \)（目標値）の差であり、小さいほど精度が高い。
（\(\ α\ \) は「極限値」だがここでは「目標値」としておこう）
n が増加して、目標値の \(α\) に数列\(a_n\) がどんどん近づき、その差が小さくなる。
その差が設定した \( \ ε \) 内に収まると、数列\(a_n\) は極限値 \(\alpha\)　に到達したことにする。
任意とは「すべて、勝手な、どれも」などの意味です。
「任意の正の数\(\ ε\)」とは勝手な小さい数です。

次の数列を例にして説明します

\( \{a_n\}=\frac{1}{1},\ \frac{1}{2},\ \frac{1}{3},\ …\frac{1}{n},\ …\)

式(2) は次のように展開できます。

\(　|a_n-α|<ε\)…(2)に対し
\(|\frac{1}{n}-0| <ε\quad \therefore \underline{n >\frac{1}{ε}} \)

目的は式(2) になるような N を求めることであるから。
上記の下線部に対して：
\(\underline{n \ge N \gt \frac{1}{ε}} \) がいえる。
（この関係から N の決められる）
これより「\(n \ge N\)なら、\(|a_n-α|<ε\)」となる。

数列が収束するイメージ
数列の番号 N を大きくすれば\( \{a_n\}\)は小さくなり、\(α\) にいくらでも近づく。　　
\( \frac{1}{n}\) もいくらでも小さくできる。

例えば\(ε=0.1\)に対して \(N=\frac{1}{0.1}=10\) が存在する。
また\(ε=0.01\)に対して \(N=\frac{1}{0.01}=100\) も存在する。
さらに\(ε=0.001\)に対して \(N=\frac{1}{0.001}=1000\) も存在する。

下図はこのイメージ
数直線上で収束近辺、下段に向けて拡大していくイメージです。

図の \(a1, a2, …an,…\) は \(\frac{1}{n_1}, \frac{1}{n_2}, … \frac{1}{n_n}, …\)のことです。
\(n=10\) なら \(a_n= \frac{1}{10}= 0.1\)です。
例えば、\(a_n= \frac{1}{10}\) (青線) を拡大して下の段に行くと「 1/10000 」（=0.0001）が見えてくる。

このように拡大するといくらでも数列は小さくできる。

このようにしてどんなに小さな正の数ε に対して

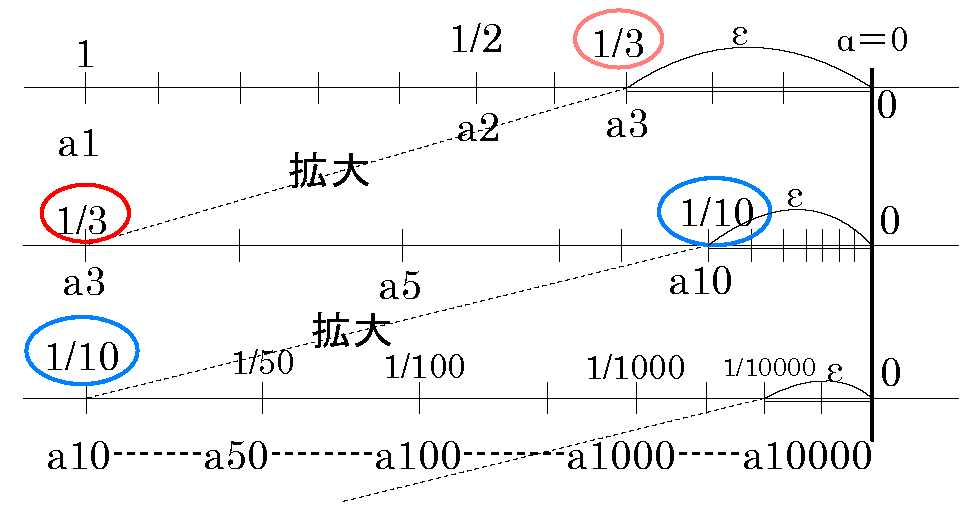
•それに対応できる数列の番号 N が決められること。
•決めた N より後のすべての項\(a_{n+k}\)について、\(ε\)より小さくでき、式(2)が成立する。

これよって「限りなく α に近づく」を使わないで「数列が α に収束する」といえることになる。

証明にあってのポイントは：

•まず、n を \(ε\)で表す関係式を作る。
•\(n \ge N\)として N と \(ε\) の関係式を作る。
•どんな小さな正の数ε にも対応できる N であることを確認。

…長い説明でしたがこれが ε-N 論法の本質です …

ε・N 論法の定義(分かり易いバージョン)

上の説明から次のように分かり易く表現します。
\(N\)、\(　n \)：自然数、\(ε\):実数
正の数 \(ε\) をどんなに小さくしても、それに対応する\(\ N\ \)があること。
（\(ε\) と \(\ N\ \)、 \(　n \) との関係式を作り N の存在を調べる。）
そして N より大きい n であれば（\(n\) が \(n≥N\) ならば）
\(|a_n-α|<ε\) が成り立つような \(N\) が見つかれば、
\(\displaystyle \lim_{ n \to \infty } \ a_n=α \) である。（数列 \(a_n\) は \(α\) に収束する。）　

例題1
数列\( a_n=\frac{1}{n} \) に対し次式が成立することをε・N 論法により証明せよ。
\(\displaystyle \lim_{ n \to \infty } \frac{1}{n}=0 \cdots (1)\)　

【証明】
証明すべき式
\(|\frac{1}{n}-0| <ε \) より
\(|\frac{1}{n}|<\varepsilon \ \)　\(\rightarrow \frac{1}{n}<\varepsilon\)　が導き出せる。
\(\therefore n>\frac{1}{\varepsilon}\)

また、「\(n \gt N \gt \frac{1}{ε}\)となる N が存在する。」のは明らかである。
\(n >N \) の関係から \(\frac{1}{n}<\frac{1}{N}\ \)である。（当たり前の関係）
\( \therefore\) \( \underline{ |\frac{1}{n}-0|\ =\frac{1}{n} < }\) \( \underline{ \frac{1}{N}<ε }　\)
つまり　どんなに小さな \(ε\) が与えられても
\( N>\frac{1}{\varepsilon} \) なる \(N\) が存在するので（※1）
\(n≥N\) ならば、 \( | \frac{1}{n}-α|<ε \)　が成り立つ。
したがって
\(\displaystyle \lim_{ n \to \infty } \frac{1}{n}=0 \)　

となる。　…証明終了。
補足（※1）：

N は自然数、ε は実数 であることに注目！
例えば\(\frac{1}{ε}=100.3\) のとき対応する自然数 \(N>101\)である。
こんなときにガウス記号[ ]を使うと以下のようになる。
\(n= [\frac{1}{ε}]+1=[100.3]+1\)\(=100+1=101\)
【ガウス記号の参照先】

例題2
数列 \( a_n=\frac{n-1}{n} \) の極限値を求めてε・N 論法により証明せよ。

\(\frac{n-1}{n}=1-\frac{1}{n}\) より極限値は「１」と推定できる。すなわち
\(\displaystyle \lim_{ n \to \infty } \frac{n-1}{n}=1 \)　を証明する。

ε・N 論法の主役の式：
\(|\frac{n-1}{n}-1| \lt ε\)　である。　これを変形して：
\(|\frac{n-1}{n}-1| \lt ε\) \(,\quad\) \(|\frac{(n-1)-n}{n}| \lt ε\)
\(|(n-1)-n| \lt nε\) \(,\quad\) \(|-1| \lt nε\) \(,\quad\) \(1\lt nε\)
\(\therefore n \gt \frac{1}{ε}\) ❶
また、「\(n \gt N \gt \frac{1}{ε}\)となる N が存在する。」は明らかである。
ここで証明を終えてもよいが（∵N の存在が分かったから）、確認もかねて次に進む。

\(n\gt N\)に対し \(\rightarrow \frac{1}{n} \lt \frac{1}{N}\)
\(N=\frac{1}{ε} \)とする（❶を満足するために）
\(|\frac{n-1}{n}-1|=\underline{\frac{1}{n} \lt \frac{1}{\color{red}{N}} }\)\(=\frac{1}{\color{red}{\frac{1}{ε}}}=ε\)
\(\therefore |\frac{n-1}{n}-1|\lt ε \)　❷　

ここで証明が終わるが、ε・N 論法風にいうと：
「以上より式❷ となるような \(n\ge N\)となる \(N\) が存在する。」となる。

【補足】

絶対値を外すと\(|a_n-α|<ε\)は:
\(\ α-ε < a_n < α+ε \quad (1)\)
\(\ a_n-ε< α < a_n+ε \quad (2)\)
と表わせる。
式(2)を数直線で描くと真ん中に\(α\)があり、その前後の\(\pm ε\)の領域があるイメージです。
この数列は \(α\) にいくらでも近づくが\(α\) にはならないことに注意。
それが式 \(|a_n-α<ε|\)　の意味、

数列が収束しないときは発散という。
発散の定義（+ ∞に発散）

\(　n, N \)：自然数、　\(K\)：実数　とする。
任意の正の（大きな）実数 K について、ある N を適当に決めると、\(n\ge N\) を満たす、すべての n について
\( a_n >K \)ならば
\(\displaystyle \lim_{ n \to \infty } a_n= + \infty \)

これを正の無限大に発散するという。

解説：
\(a_n\) が限りなく大きくなるから、どんなに大きな K があっても、それに対してn を適当に決めれば \(a_n\) はさらに大きくなる。
すなわち\(a_n\) はいくらでも大きくなることを意味する。
これにより曖昧な「限りなく大きくなる」を使わないで表現したことになる。

発散の定義（- ∞に発散）

任意の正の（小さな）実数 M について、ある N を適当に決めると、\(n\ge N\) を満たす、すべての n について
\( a_n <K \)ならば
\(\displaystyle \lim_{ n \to \infty } a_n= - \infty \)

これを負の無限大に発散するという。

発散数列の例

\(\displaystyle \lim_{ n \to \infty } n=+ ∞ \)

\(\displaystyle \lim_{ n \to \infty } -(a^n)=- ∞ \) \( \quad( a\gt 0) \)　

\(\displaystyle \lim_{ n \to \infty } (-a)^n= \pm \infty \) \( \quad( a\gt 0) \)　
（上記は振動現象…これも発散と呼ぶ）

例題3
\(\displaystyle \lim_{ n \to \infty } 2n=+ \infty \)

ε・N 論法により証明せよ。

任意の実数 K について \(2n\gt K\)　から n を求めと
\(n \gt \frac{K}{2} \) である。
したがって \(n \gt N \gt \frac{K}{2}\) となる N を適当に決めれば
\(n \gt N \) となるような n について \(2n\gt K\) が成り立つ。
\(\therefore \displaystyle \lim_{ n \to \infty } 2n=+ \infty \)

例題4
\( \displaystyle \lim_{ n \to \infty } -(b)^n=- \infty \) \(\quad (b\gt 0)\)

ε・N 論法により証明せよ。

任意の実数 K について \( -(b)^n \lt K\)　から n を求める。

K は負であること、(-K)は正であることに注意
\( b^n \gt -K\)
上記の指数を対数表示すると：
\(n \gt log_b (-K) \)　（基底はb）　となる。

\(n \gt log_b (-K) \)
したがって \(n \gt N \gt log_b (-K) \) となる N を適当に決めれば
\(n \gt N \) となるような n について \( -(b)^n \lt K\) が成り立つ。
\(\therefore \displaystyle \lim_{ n \to \infty } -(b)^n=- ∞ \)

coffe

[コーヒーブレイク/閑話］…お疲れさまでした

1.「ε-N 論法」の名前は小文字の「\(n\)」でなく、大文字の「\(N\)」です。

この論法では \(ε\)に依存する \(N\) を求めること、\(N\) は\(ε\) の関数として \(N(ε)\) と表わしている本もある。

2.ε-N 論法の英語版

1. 【参考先】
For any \(ε \gt 0\), there exists a natural number N(ε)　
such that for all \( n \geq N(ε)\), we have \(|a_n-\alpha| \gt ε\)
(ε is real number)

2. 【参考先】
For each real number \(ε \gt 0\), there exists a natural number N such that,
for every natural number \( n \geq N\), we have \(|a_n-\alpha| \gt ε\)