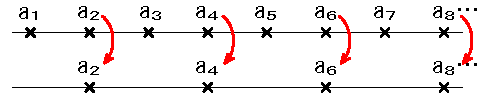
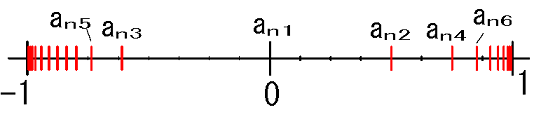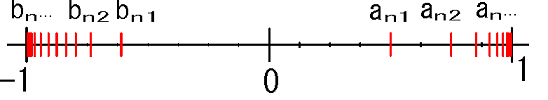もとの数列:
\(\{a_n\}=a_1,a_2,a_3,a_4,a_5,a_7,\cdots\)に対し
この部分列:
\( \{ a_{n_{k}} \}=a_{n_{1}},a_{n_{2}},a_{n_{3}},\cdots\)\(=a_2,a_4,a_6,,\cdots\)
これは元の数列の偶数番である \(n_k=2k\) の規則にある部分列です。
例2
奇数番となる部分列を作る
もとの数列:
\(\{a_n\}=a_1,a_2,a_3,a_4,a_5,a_7,\cdots\)に対し
\(n_k=2k+1\) の関係にある部分列です。
例3
発散数列でも部分列では収束する
上図の数列は
\(a_n=(-1)^n (1-\frac{1}{n})\)
fig2 の通り この数列はn を大きくすると-1 と1 に振動(発散)します。
しかし、この数列を次のように表し:
\( a_{n_{k}}\)\(=(-1)^{n_{k}}(1-\frac{1}{ {n_{k}}} ) \)
以下の部分列をとると収束します。
•
\({n_{k}}=2k\)として(偶数)
\( a_{2k}\)\(=(-1)^{2k} (1-\frac{1}{2k}) \)
fig3 の右側:この部分列は1 に収束します。
•
\({n_{k}}=2k-1\)として(奇数)
\( b_{2k-1}\)\(=(-1)^{2k-1} (1-\frac{1}{2k-1}) \)
fig3 の左側:この部分列は-1 に収束します。
この講義では使いませんが、集積値を用いている本もあるので紹介しておきます。
集積値とは
数列\(\{a_n\}\)のある部分列が点α に収束するとき、このα を数列\(\{a_n\}\)の集積値(点)という。
例をあげると
•\(a_n=(-1)^n (1-\frac{1}{n})\) →fig2
集積値は-1 と1 の2つ。
この数列の以下の2つの
部分列では
•\( a_{2k}\)\(=(-1)^{2k} (1-\frac{1}{2k}) \) →fig3 の右側
集積値は1。(極限値と同じ)
•\( b_{2k-1}\)\(=(-1)^{2k-1} (1-\frac{1}{2k-1}) \) →fig3 の左側
集積値は-1。(極限値と同じ)
ここでは1次元の数列の集合ですが、2次元\(R^2\)のときはx-y座標の2変数(2つの要素)の実数で定まる点集合です。
その点は \(a_{ij}(x_i,y_j)\)で表わされる。点集合が有界のとき、集合の点は一定の有限範囲内にあり、平面上の円内(または正方向形内)にあります。
1つの点集合S についてある点A が集積点とは A の
どれほどの近いところにも S の元となる点が無数にあるときをいいます。
点A を囲む近い円にS の点が無数あり、さらに点A に近い円にもS の点が無数あるということです。
(円をどんどん小さくしてもS の点が無数ある)
「近い」とは距離のこと、下式の距離\(AP\)のことです。
点A\(=(a,b)\),S の点P\(=(x,y)\)とすると:
距離\(AP=\sqrt{(a-x)^2+(b-y)^2}\)
(三平方の定理)
単調性と有界
実数の連続性と同値な定理の一つに「有界な単調数列の収束」の定理があります。
・上に有界な単調増加数列は(上限に)収束する。
・下に有界な単調減少数列は(下限に)収束する。
例として、次の数列を調べてみましょう!
\( a_n= ( 1+ \frac{1}{n})^n \)
\(\ :ⓐ\)
この数列はネピア数e を与える数列です。
\(\displaystyle \lim_{n \to \infty} ( 1+ \frac{1}{n})^n=e \)\(=2.718281\cdots\)
この例はe の値を求めることではありません。
単調性を調べる
2項定理を使い展開する:
\(a_n = \displaystyle \sum_{ r = 0 }^{ n } \ {}_n \mathrm{ C }_r (1 + \frac{1}{n})^n \)
\(= {}_n \mathrm{ C }_0\cdot 1^n + {}_n \mathrm{ C }_1\cdot 1^{n-1} \frac{1}{n} + {}_n \mathrm{ C }_2 \cdot 1^{n-2}\frac{1}{n^2}\) \(+ {}_n \mathrm{ C }_3 \cdot 1^{n-3}\frac{1}{n^3}\)
\( + \cdots + {}_n \mathrm{ C }_r \cdot 1^r \frac{1}{n^r}\)
\( +\cdots +{}_n \mathrm{ C }_{n} \frac{1}{n^{n}}\)
\(= 1 + n \frac{1}{n} + \frac{n(n-1)}{2!} \frac{1}{n^2} \) \(+ \frac{n(n-1)(n-2)}{3!} \frac{1}{n^3} \)
\( \cdots + \color{red} {\frac{1}{n^n}} \) \(\quad :ⓐ'\)
上式の最終項
\(= \color{red} { \frac{1}{n^n}} = \frac{n!}{n!} ( \frac{1}{n^n})\)
\(=\frac{1}{n!} \cdot (1-\frac{1}{n}) \cdot (1-\frac{2}{n}) \cdots \cdot (1-\frac{(n-1)}{n}) \)
\(=1 + 1 + \frac{1}{2!}(1-\frac{1}{n}) \) \(+ \frac{1}{3!} (1-\frac{1}{n}) (1-\frac{2}{n}) \)
\(+ \cdots + \frac{1}{n!} \cdot (1-\frac{1}{n}) \cdot (1-\frac{2}{n}) \cdots (1-\frac{n-1}{n}) \)
\(\quad :ⓐ''\)
n を n+1 に置き換えて \( a_{n+1} \) を計算する。
\( a_{n+1} = 1 + 1 + \frac{1}{2!}(1-\frac{1}{n+1}) \)
\(+ \frac{1}{3!} (1-\frac{1}{n+1}) (1-\frac{2}{n+1}) \)
\(+ \cdots + \frac{1}{n!} \cdot (1-\frac{1}{n}) \cdot (1-\frac{2}{n}) \cdots (1-\frac{n-1}{n}) \)
\(+ \underline{\frac{1}{(n+1)!} \cdot (1-\frac{1}{n+1}) \cdot (1-\frac{2}{n+1}) \cdots (1-\frac{n}{n+1})} \)
各項を注視すると、
\( a_n \)と比べ\( a_{n+1}\)
の各項の値は大きく、また項(最終の下線部)が1つ増えている。
\( \therefore a_{n+1} ≥ a_n \)
\( a_n \)
は単調増加数列である。
次の関係がなりたちます(はじめは式ⓐ''とおく)
\(a_n=ⓐ''= 1 + 1 + \frac{1}{2!}(1-\frac{1}{n}) \) \(+ \frac{1}{3!} (1-\frac{1}{n}) (1-\frac{2}{n}) \)
\(+ \cdots + \frac{1}{n!} \cdot (1-\frac{1}{n}) \cdot (1-\frac{2}{n}) \cdots (1-\frac{n-1}{n}) \)
<
\(1+1+ \frac{1}{2!} +\frac{1}{3!} + \frac{1}{4!}+\cdots+\frac{1}{(n-1)!}+\frac{1}{n!}\)
<
\(1+ \underline{1+ \frac{1}{2} +\frac{1}{2^2} + \frac{1}{2^3}+\cdots+\frac{1}{2^{n-2}}+\frac{1}{n^{n-1}} }\)
:ⓑ
・\(2^{n-1}\)
と
\(n!\)
の大小関係は:(式ⓑの根拠)
\(2^{n-1}=1\cdot2^{n-1} \lt n!\) \(=1 \cdot 2\cdot 3\cdot \cdots (n-1) \cdot n \)
逆数であることに注意
・式ⓑの下線部は等比数列です。
初項=1、公比
\(r=\frac {1}{2}\)
\( S_n=\frac{1-(\frac{1}{2})^n}{1-\frac{1}{2}} \)
これを反映させると次のようになる。
\(a_n\)\(\lt 1+\underline{1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots} \)
\( \underline{ \cdots+\frac{1}{2^{n-2}}+\frac{1}{n^{n-1}} }\)
\(\lt 1+ \frac{1-(\frac{1}{2})^n}{1-\frac{1}{2}} \)
\( = 1+ 2(\frac{2^2-1}{2^2}) \)
\( = 1+2(1-\frac{1}{2^n})\)
\( = (3-\underline{\frac{1}{2^{n-1}}} ) \lt 3\)
(\(0\lt 下線部\le 1\) )
以上よりの結果:
\(2\le a_n \lt 3\)
\(a_n\) は下は2、上は3 で抑えられている。
これより数列 \(a_n\) は上に有界、単調増加であるから収束数列です。
このように収束先は判らないが収束数列であることがわかります。
コーシー列の定義
任意の正の実数εに対しある自然数N (\(\in \bm{N}\)) が存在し\(m,n \ge N\) ならば、すべての\(m,n\) について
\(|a_m-a_n|\ltε\)
となるとき 数列\( \{a_n\} \) はコーシー列(基本列ともいう)であるという。
補足:
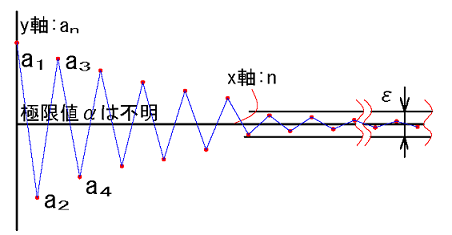
・m とn を大きくしていくと\(a_n\)と\(a_m \)の差が小さくなり収束していくイメージです。
・収束先の情報はありません。(極限値α が不明な状況)
コーシー列の収束条件定理
数列\( \{a_n\} \)が収束するには\( \{a_n\} \)が次のコーシー列の条件© を満たすことが必要で十分である。
\( \forall ε\quad \exists N\in \bm{N}\quad s.t.\ \forall m,n\in{\bm{N}}\)\(\quad ( m,n\ge N ⇒ |a_m-a_n|\ltε)\)
:©
補足
・論理式© の内容は定義と同じ、またコーシー列を示すものです。
上記の定理を次の2つに分けて証明します。
➀\(\{a_n\}\)が収束する⇒コーシー列である
➁収束する⇐\(\{a_n\}\)がコーシー列
これを1行に表わすと:
\(\{a_n\}\)が収束 \( \Leftrightarrow\) \(\{a_n\}\)がコーシー列
コーシー列の定理➀
➀収束するならコーシー列である。
(➀\(\{a_n\}\)が収束する ⇒ コーシー列である)
【証 明】
数列\(\{a_n\}\) は収束するとする。
すなわち
\(\displaystyle \lim_{n \to \infty} a_n=α\)
(仮定)である。
任意の正の実数ε に対し、ある\(N\in \bm{N}\)が存在して \( m,n\le N \) であるすべての m,n について
\( \quad \) \(|a_m-α|\ltε\)\( \quad \) \( |a_n-α|\ltε\)
である。
\(|a_m-a_n|\) は次のように展開できる:
\(|a_m-a_n|\) \(=\ul{|(a_m-α)+(α-a_n)|}\)\(\ul{\le |a_m-α|+|a_n-α|}\)\(\lt2ε=ε'\)
下線部は三角不等式
∴「➀収束するならコーシー列である。」
コーシー列の定理➁(実数の完備性)
➁コーシー列なら収束する
(➁収束する ⇐ コーシー列であるなら)
【実数の完備性】ともいう
この性質は実数の連続性に基いていて、\(\{a_n\}\) がコーシ―列でもあっても有理数では収束するとは限らない。
(例えば \(\sqrt{2}\)に収束する有理数はない)
この性質は実数全体の集合\(\bm{R}\) が備えている特徴であり、こいうことから「実数の完備性」と呼ばれている。
次の2つのことを証明します。
・コーシー列は有界であること。
・コーシー列なら収束すること。(※)
※:ボルツァーノ・ワイエルシュトラスの定理を利用する。
1)コーシー列は有界であることの証明
数列\(\{a_n\}\) は十分遠くにいくと(n を大きくすると)、\(\{a_n\}\)の各項はお互いに近くにいる状態です。
すなわち、\(\{a_n\}\)の各項の差は、十分小さな\(ε\) に収まるようになる。
コーシー列の定義より
\(m,n \ge N (\in \bm{N})\) ならば、すべての\(m,n\) について
\(|a_m-a_n|\ltε\)
において
n を\(n=N+1\) として固定し、式展開すると:
\(|a_m-a_{N+1}|\ltε\)
\(-ε\lt|a_m-a_{N+1}|\ltε\)
\(a_{N+1}-ε \lt a_m \lt a_{N+1}+ε\)
N個以上の無限個ある数列について:
\(a_m\)は
\(a_{N+1}-ε\):下界、
\( a_{N+1}+ε\):上界
として有界である。
注:またN個以下の有限個ある数列も最小/最大の数列があるから有界である。
∴コーシー列は有界である。
この証明には、
前回習った「ボルツァーノ・ワイエルシュトラス(B・W)の定理」を利用します。
実数の数列\(\{a_n\}\) が有界であるとき、\(\{a_n\}\)は収束する部分列\(\{a_{n(k)}\}\)をもつ。
コーシ―列に部分列が存在します。
コーシ―列は有界だから B・W の定理より収束部分列\(\{a_{n(k)}\}\)が存在します。
ここで
\(\displaystyle \lim_{k\to \infty} a_{n(k)}=α\)
とする。(仮定)
証明することは
\(|a_n-α|\lt ε'\)
です。
このために以下のことを使います。
•収束部分列の収束とは
\(k \in \bm{N}\) が存在し\( \ul{k\ge K} ⇒\ul{|a_{n(k)}-α|\lt ε}\)
:ⓐ
•コーシ列の収束とは
\(N_1 \in \bm{N}\) が存在し \( \ul{m,n\ge N_1} ⇒\ul{|a_m-a_n|\lt ε}\)
:ⓑ
ここで\(\ul{N=max \{K,N_1\}}\)
:© とおいて
(\(N はK と N_1\) のいずれか大きいほう)
\(\ul{ n\gt N} \)
:ⓓ のとき
\(|a_n-α|= |(a_n-a_{n(N)})+(a_{n(N)}-α| \)
\(\le \underbrace{|a_n-a_{n(N)}|}_{Ⓐ}+\underbrace{|a_{n(N)}-α|}_{Ⓑ} \)
概略:(詳細は
後述(※))
上式「\(\cdots \le |Ⓐ|+|Ⓑ|\)」 は三角不等式。
Ⓐ は数列の添字が\(N_1\)以上だからε 以下。
Ⓑ は数列の添字が\(K \)以上だからε 以下。
\(\therefore |a_n-α|\le\)
\(=ε+ε=ε'\)
これより
コーシ列は収束します。
また1),2)の結果から、次のように両方向が成り立ちます。
\(\{a_n\}\)が収束 \( \Leftrightarrow\) \(\{a_n\}\)がコーシー列
詳 細(※):
Ⓐ項 \(|a_n-a_{n(N)}|\) について
\(a_n\)の添字は式ⓑ,©より:\(\to n\ge N\ge N_1\)
\(a_{n(N)}\)の添字:
(部分列は元の数列の一部を取り出すから)
・添字の番号は「部分列\(\ge\)元の数列」だから
\(n(N)\ge k \ \Rightarrow \ n(N)\ge N\)
・\(n(N)\ge N\ge N_1\)
これより
\(a_n\)と\(a_{n(N)}\)は\(N_1\)以上の大きい数だからⒶ項は収束します。
Ⓑ項 \(|a_{n(N)}-α|\) について
\(a_{n(N)}\)の添字は上記のとおり \(n(N)\ge N\ge N_1\)だから
式ⓐ と同じになるからⒷ項は収束します。