力学の多くの教科書では「角運動量を \(\bm{L} = \bm{r}\times\bm{p}\) と定義する」から始まる。
\(\bm{L}\) は\(\bm{r}\) と \(\bm{p}\) に垂直で, 多くは\(\ z \) 軸に向かうベクトルと説明される。
\(\ z_{-}\) か\(\ z_{+}\)かは, 右手系か左手系で, どちらに定義しても良い。
では\(\ z \) 軸方向にはどのような物理的な作用があるのだろうか?同じベクトル積で表されるローレンツ力,
\[\bm{f} = q\Vec\upsilon\ × \bm{B~}\]
では, 荷電粒子は, 実際に磁場\(\bm{B}\)と運動方向 \(\Vec\upsilon\) に垂直な力を受ける。
コマが立っていられるのは「遠心力で軸の周りに均等に引かれているから」と説明する著名な大学教授もおられるらしい。さすがにそれはないだろう!が, コマの軸方向を指さし「この方向に角運動量の力が働いている」と説明された教授もおられるし, そのような文献も見ることができる。角運動量が\(\ z~\) 軸方向に力を加えていると, 数年間, 真面目に考えていた。
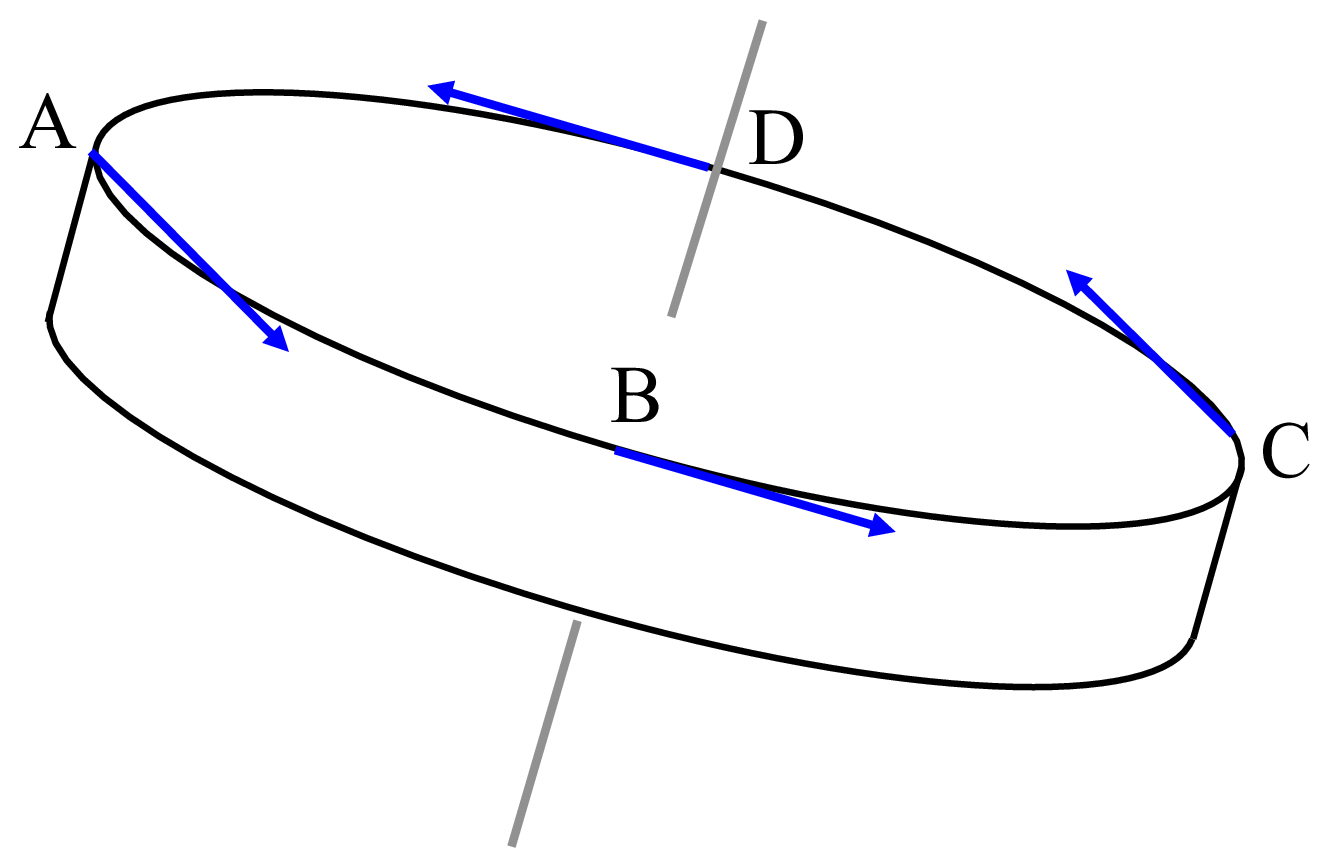
しかし, この考えは簡単に否定される。垂直に回っているコマを倒すと, 図のAとCでは運動量の向きは水平で変わらないが, Bは下向きに, Dは上向きに大きく変わる。コマの軸を傾けるには力が必要である。角運動量が軸を垂直に引っ張っているなどと, 怪しい議論は必要ない。
角運動量の向きに実体は無い。そう言えば「運動量保存則」からは「作用反作用の法則」が導かれるが, 角運動量にはそのような公理に近いものは無い。外積のルールに従う必要はあるのだろうか? そもそも角運動量をベクトルにして問題は起きないのだろうか?
以下はゴールドスタイン古典力学, 4章剛体の運動学の一部の要約である。詳しくは同著を参照されたい。オイラー角を用いた詳細な議論がある。
無限小回転の数理
回転は行列で表現できる。例えば\(\ z \) 軸周りの回転は, 以下のように表される。
\[
T =
\begin{pmatrix}
\cos\phi & \ -\sin\phi & {0} \\
\sin\phi & \cos\phi & {0} \\
{0} & {0} & {1} \\
\end{pmatrix}
\]
\(\ T\)はいわゆる直交行列(成分が複素数の場合はユニタリ行列)で, 直交行列には, ベクトルの長さを変えない, ベクトル間の角度を変えないという性質があり, その性質を利用して, 基底変換に用いられる事が多い。そして, その逆行列と転置行列が等しい。
\[A^{-1}=A^{t}\tag{1}\]
ここで\(\ A\) を無限小回転行列とすると, \(\ A\) は単位行列\(\ E\) と微小回転部分 \(\varepsilon\) を用いて
\[A=E+\varepsilon\]
として良いだろう。\(\ A\) の逆行列は\(A^{-1}=E-\varepsilon~\)だとすぐ分かる。なぜならば,
\[AA^{-1}=(E+\varepsilon)(E-\varepsilon)=E^{2}-\varepsilon^{2}=E\]
だからである。ここで \(\varepsilon^{2}\) は十分に小さいので無視した。
\(A^{-1}=E-\varepsilon, A^{t}=(E+\varepsilon)^{t}=E^{t}+\varepsilon^{t}=E+\varepsilon^{t}\)
だから(1)より
\[-\varepsilon = \varepsilon^{t}\]
である。このような行列を反対称行列と呼ぶ。一般性を失わずに,
\[
\varepsilon = d\Omega =
\begin{pmatrix}
0 & -d\Omega_{3} & d\Omega_{2} \\
d\Omega_{3} & 0 & -d\Omega_{1}\\
-d\Omega_{2} & d\Omega_{1} & 0 \\
\end{pmatrix}
\]
として良い。突然\(\Omega\)が出てきたのは, 角速度ベクトル, \[\Vec\omega=\frac{d\Vec\Omega}{dt}\]を導きたいからである。
無限小回転した時の位置ベクトルの変位\(\ d\bm{r~}\)は, 変位後のベクトルを\(\bm{~r'}\)とすれば
\[d\bm{r}=\bm{r'}-\bm{r}=(E+\varepsilon)\bm{r}-\bm{r}=\varepsilon\bm{r}\]
である。位置ベクトルを\(\bm{r}(x,y,z)\)とすれば,
\[
\begin{align}
d\bm{r} &=
\begin{pmatrix}
0 & -d\Omega_{3} & d\Omega_{2} \\
d\Omega_{3} & 0 & -d\Omega_{1}\\
-d\Omega_{2} & d\Omega_{1} & 0 \\
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}\\
&=
\begin{pmatrix}
zd\Omega_{2}-yd\Omega_{3} \\
xd\Omega_{3}-zd\Omega_{1} \\
yd\Omega_{1}-xd\Omega_{2} \\
\end{pmatrix}\\
\end{align}
\]
である。どこかで見た外積の計算である。幸い行列\(~d\Omega~\)の独立成分が3つなので, これをベクトルと見て,
\[
d\b\Omega=
\begin{pmatrix}
d\Omega_{1} \\
d\Omega_{2} \\
d\Omega_{3} \\
\end{pmatrix}\\
\]
とすると\(\ d\bm{r~}\)は(\(d\Omega\)は行列, \(d\b\Omega\)はベクトル)
\[
\begin{align}
d\bm{r}&=d\b{\Omega~}\x\bm{~r}\\
&=
\begin{pmatrix}
d\Omega_{1} \\
d\Omega_{2} \\
d\Omega_{3} \\
\end{pmatrix}
\x
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}\\
&=
\begin{pmatrix}
zd\Omega_{2}-yd\Omega_{3} \\
xd\Omega_{3}-zd\Omega_{1} \\
yd\Omega_{1}-xd\Omega_{2} \\
\end{pmatrix}\\
\end{align}
\]
と外積の計算ルールに従っていることが分かる。改めて書き直すと,
\[d\bm{r} =d\b\Omega~\x\bm{~r}\tag{2}\]
直交変換なので, \(\bm{~r~}\)の大きさは変わらないとして(2)の両辺を\(\ dt\)で割ると, 質点の速度
\(\Vec\upsilon\) は
\[\Vec\upsilon = \frac{d\b{r}}{dt}= \frac{d\Vec\Omega}{dt}\x\b{r}=\Vec\omega\x\b{r}\]
\(\Vec\omega~\)を角速度ベクトルと呼ぶ。速度 \(\Vec\upsilon\) は, ベクトル積 \(\Vec\upsilon = \Vec\omega\x\bm{r~}\)で表される。
細字をスカラー, 太字をベクトルとすると, 角運動量は次のように表される。
\[
\bm{L}=r\cdot\bm{p}=r\cdot\ m\Vec\upsilon=rm\cdot\Vec\omega\x\bm{r}=(mr)~\Vec\omega\x\bm{r}
\]
面倒なのでこれを\(~\bm{L}=\bm{r}\x \bm{p~}\)と書く。
無限小回転\(~d\Omega~\)をベクトルと見立てたところから導かれるので, 角速度ベクトル \(\Vec\omega~\)の方が基本である。\(\Vec\omega~\)にしても実体の無いのは同じである。
以上が, 角運動量をベクトル積を用いて \(\bm{L} = \bm{r}\x \bm{p}\) とする理由である。
角速度ベクトルは, ロドリゲスの回転公式からも同様の結果が得られるが, 量子力学で決定的役割を果たす角運動量, スピン角運動量は, 無限小回転から導かれる。(J.Jサクライ現代の量子力学3章)
軸性ベクトルと極性ベクトル
さてベクトルには物理的実体のあるものと, 数学的便宜のために導入されたものとがあることが分かった。実体のある前者を極性ベクトルと呼ぶ。実体のない後者は数学では擬ベクトル, 物理では軸性ベクトルと呼ぶことが多い。極性ベクトルは, 位置\(\bm{r}\), 速度\(\Vec\upsilon\), 運動量\(\bm{~p~}\), 電界\(\bm{E~}\)などであり, 擬ベクトルは角運動量\(\bm{L}\), 力のモーメント\(\bm{N}\), 磁束密度\(\bm{B~}\)などである。
回転が頭から離れない物理学者は "軸性ベクトル" と名付けたが, 物体に興味のない数学者は, 情け容赦なく
"擬" ベクトルと名付けた。(本当か?)
ともあれこれですっきりした。これからは安心して \(\bm{L} = \bm{r}\x \bm{p}\) を使おう。外積だよ!